Đề thi giữa kì 1 Toán 7 - Đề số 11
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Đề bài
Kết quả phép tính \(0,5 + \frac{3}{{ - 4}}\) là
-
A.
\(\frac{7}{4}\).
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{{ - 1}}{4}\).
-
D.
\(\frac{{ - 19}}{8}\).
Cách biểu diễn số \(\frac{3}{4}\) trên trục số nào dưới đây đúng?
-
A.
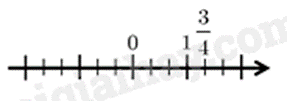
-
B.
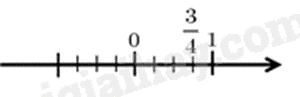
-
C.
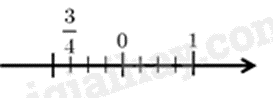
-
D.

Tập hợp số hữu tỉ được kí hiệu là
-
A.
\(\mathbb{N}\).
-
B.
\(\mathbb{Z}\).
-
C.
\({\mathbb{N}^*}\).
-
D.
\(\mathbb{Q}\).
Giá trị của \({({2^3})^2}\) bằng
-
A.
4.
-
B.
8.
-
C.
64.
-
D.
16.
Trong các số hữu tỉ \(\frac{{ - 1}}{2};\frac{{ - 3}}{4};0;1;\frac{1}{2};\frac{4}{3}\) có bao nhiêu số hữu tỉ dương?
-
A.
2.
-
B.
3.
-
C.
4.
-
D.
5.
Điền kí hiệu thích hợp vào ô trống: \( - \frac{7}{6}{\rm{ }}...{\rm{ }}\mathbb{Q}\)
-
A.
$\in $.
-
B.
$\notin $.
-
C.
$=$.
-
D.
$<$.
Số nghịch đảo của số − 0,7 là
-
A.
0,7.
-
B.
\(\frac{{ - 7}}{{10}}\).
-
C.
\( - \frac{{10}}{7}\).
-
D.
\(\frac{{10}}{7}\).
Kết quả của phép tính \({\left( {\frac{{ - 3}}{4}} \right)^8}.{\left( {\frac{{ - 3}}{4}} \right)^2}\) là
-
A.
\({\left( {\frac{{ - 3}}{4}} \right)^6}\).
-
B.
\({\left( {\frac{{ - 3}}{4}} \right)^{10}}\).
-
C.
\({\left( {\frac{{ - 3}}{4}} \right)^4}\).
-
D.
\({\left( {\frac{{ - 3}}{4}} \right)^{16}}\).
-
A.
\(90^\circ \).
-
B.
\(60^\circ \).
-
C.
\(45^\circ \).
-
D.
\(30^\circ \).
Hình lăng trụ đứng tam giác có số cạnh là
-
A.
8.
-
B.
12.
-
C.
9.
-
D.
10.
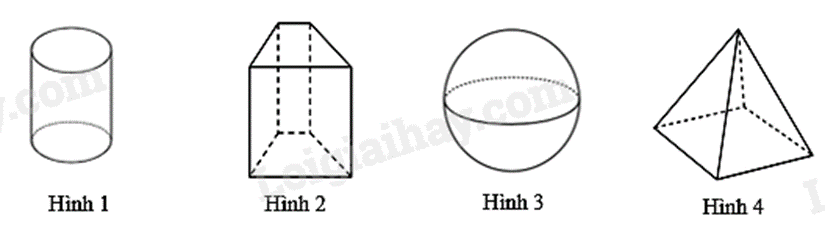
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
-
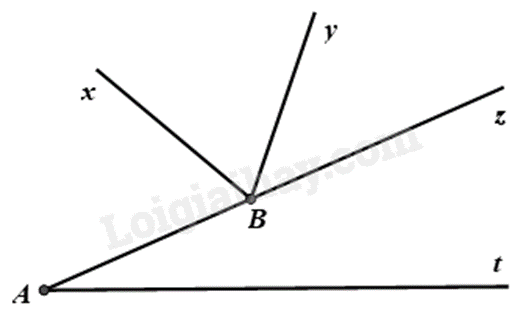
A.
\(\widehat {xBy}\) và \(\widehat {yBz}\) là hai góc kề nhau.
-
B.
\(\widehat {xBz}\) và \(\widehat {yBz}\) là hai góc kề bù.
-
C.
\(\widehat {yBz}\) và \(\widehat {zAt}\) là hai góc kề nhau.
-
D.
\(\widehat {ABy}\) và \(\widehat {xBz}\) là hai góc đối đỉnh.
Lời giải và đáp án
Kết quả phép tính \(0,5 + \frac{3}{{ - 4}}\) là
-
A.
\(\frac{7}{4}\).
-
B.
\(\frac{1}{4}\).
-
C.
\(\frac{{ - 1}}{4}\).
-
D.
\(\frac{{ - 19}}{8}\).
Đáp án : C
Đưa 0,5 về phân số, thực hiện phép cộng với hai số hữu tỉ.
Ta có: \(0,5 + \frac{3}{{ - 4}} = \frac{1}{2} + \frac{{ - 3}}{4} = \frac{2}{4} + \frac{{ - 3}}{4} = \frac{{ - 1}}{4}\).
Đáp án C .
Cách biểu diễn số \(\frac{3}{4}\) trên trục số nào dưới đây đúng?
-
A.

-
B.
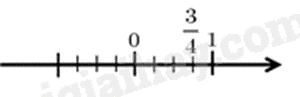
-
C.

-
D.

Đáp án : B
Dựa vào cách biểu diễn số hữu tỉ trên trục số.
Biểu diễn số hữu tỉ \(\frac{3}{4}\) trên trục số.
Chia đoạn thẳng đơn vị thành 4 phần bằng nhau. Lấy một đoạn làm đơn vị mới (đơn vị mới bằng \(\frac{1}{4}\) đơn vị cũ)
Số hữu tỉ được biểu diễn bằng điểm nằm bên phải gốc O, cách gốc O một đoạn bằng 3 đơn vị mới.
Do đó hình B biểu diễn số \(\frac{3}{4}\).
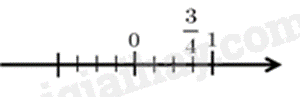
Đáp án B .
Tập hợp số hữu tỉ được kí hiệu là
-
A.
\(\mathbb{N}\).
-
B.
\(\mathbb{Z}\).
-
C.
\({\mathbb{N}^*}\).
-
D.
\(\mathbb{Q}\).
Đáp án : D
Dựa vào kí hiệu các tập hợp.
Tập hợp các số hữu tỉ được kí hiệu là \(\mathbb{Q}\).
Đáp án D .
Giá trị của \({({2^3})^2}\) bằng
-
A.
4.
-
B.
8.
-
C.
64.
-
D.
16.
Đáp án : C
Dựa vào kiến thức lũy thừa của lũy thừa: \({\left( {{a^m}} \right)^n} = {a^{m.n}}\).
Ta có: \({({2^3})^2} = {2^{3.2}} = {2^6} = 64\).
Đáp án C .
Trong các số hữu tỉ \(\frac{{ - 1}}{2};\frac{{ - 3}}{4};0;1;\frac{1}{2};\frac{4}{3}\) có bao nhiêu số hữu tỉ dương?
-
A.
2.
-
B.
3.
-
C.
4.
-
D.
5.
Đáp án : C
Số hữu tỉ dương là các số hữu tỉ lớn hơn 0.
Có 4 số hữu tỉ dương, đó là: \(0;1;\frac{1}{2};\frac{4}{3}\).
Đáp án C .
Điền kí hiệu thích hợp vào ô trống: \( - \frac{7}{6}{\rm{ }}...{\rm{ }}\mathbb{Q}\)
-
A.
$\in $.
-
B.
$\notin $.
-
C.
$=$.
-
D.
$<$.
Đáp án : A
Dựa vào kiến thức về các kí hiệu \( \in , \notin \).
Vì \( - \frac{7}{6}\) là số hữu tỉ nên \( - \frac{7}{6}{\rm{ }} \in {\rm{ }}\mathbb{Q}\).
Đáp án A .
Số nghịch đảo của số − 0,7 là
-
A.
0,7.
-
B.
\(\frac{{ - 7}}{{10}}\).
-
C.
\( - \frac{{10}}{7}\).
-
D.
\(\frac{{10}}{7}\).
Đáp án : C
Hai số được gọi là nghịch đảo nếu tích của chúng bằng 1.
Ta có: \( - 0,7 = - \frac{7}{{10}}\); \(\left( { - \frac{7}{{10}}} \right).\left( { - \frac{{10}}{7}} \right) = 1\) nên số nghịch đảo của \( - 0,7\) là \( - \frac{{10}}{7}\).
Đáp án C .
Kết quả của phép tính \({\left( {\frac{{ - 3}}{4}} \right)^8}.{\left( {\frac{{ - 3}}{4}} \right)^2}\) là
-
A.
\({\left( {\frac{{ - 3}}{4}} \right)^6}\).
-
B.
\({\left( {\frac{{ - 3}}{4}} \right)^{10}}\).
-
C.
\({\left( {\frac{{ - 3}}{4}} \right)^4}\).
-
D.
\({\left( {\frac{{ - 3}}{4}} \right)^{16}}\).
Đáp án : B
Sử dụng kiến thức tích hai lũy thừa cùng cơ số: \({a^m}.{a^n} = {a^{m + n}}\).
Ta có:
\({\left( {\frac{{ - 3}}{4}} \right)^8}.{\left( {\frac{{ - 3}}{4}} \right)^2} = {\left( {\frac{{ - 3}}{4}} \right)^{8 + 2}} = {\left( {\frac{{ - 3}}{4}} \right)^{10}}\).
Đáp án B .
-
A.
\(90^\circ \).
-
B.
\(60^\circ \).
-
C.
\(45^\circ \).
-
D.
\(30^\circ \).
Đáp án : D
Dựa vào kiến thức về hai góc đối đỉnh và hai góc kề nhau.
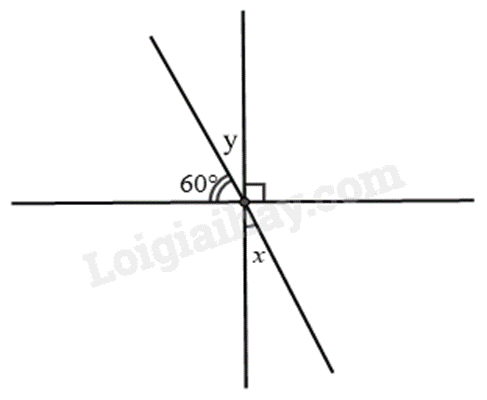
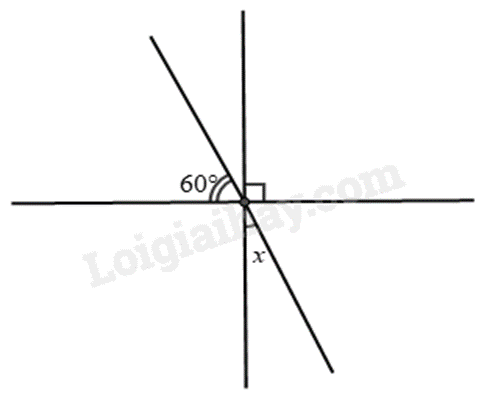
Ta đặt góc \(y\) như hình vẽ.
Vì \(y + 60^\circ = 90^\circ \) nên \(y = 90^\circ - 60^\circ = 30^\circ \).
Vì \(x\) và \(y\) là hai góc đối đỉnh nên \(x = y = 30^\circ \).
Đáp án D .
Hình lăng trụ đứng tam giác có số cạnh là
-
A.
8.
-
B.
12.
-
C.
9.
-
D.
10.
Đáp án : C
Dựa vào đặc điểm của hình lăng trụ đứng tam giác.
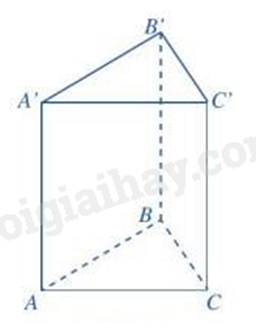
Hình lăng trụ đứng tam giác có 9 cạnh.
Đáp án C .
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Đáp án : B
Dựa vào kiến thức về hình lăng trụ đứng tứ giác.
Hình 2 là hình lăng trụ đứng tứ giác.
Đáp án B .
-
A.
\(\widehat {xBy}\) và \(\widehat {yBz}\) là hai góc kề nhau.
-
B.
\(\widehat {xBz}\) và \(\widehat {yBz}\) là hai góc kề bù.
-
C.
\(\widehat {yBz}\) và \(\widehat {zAt}\) là hai góc kề nhau.
-
D.
\(\widehat {ABy}\) và \(\widehat {xBz}\) là hai góc đối đỉnh.
Đáp án : A
Dựa vào kiến thức về hai góc kề nhau, hai góc kề bù, hai góc đối đỉnh.
\(\widehat {xBy}\) và \(\widehat {yBz}\) là hai góc kề nhau là khẳng định đúng.
\(\widehat {xBz}\) và \(\widehat {yBz}\) không phải là hai góc kề bù.
\(\widehat {yBz}\) và \(\widehat {zAt}\) không phải là hai góc kề nhau.
\(\widehat {ABy}\) và \(\widehat {xBz}\) không phải là hai góc đối đỉnh.
Đáp án A .
a) Đưa các hỗn số về phân số để thực hiện phép tính với số hữu tỉ.
b) Sử dụng tính chất phân phối của phép nhân đối với phép cộng.
c) Thực hiện phép tính với lũy thừa.
d) Thực hiện phép tính với lũy thừa.
a) \(1\frac{2}{5} + 3\frac{3}{5}\)
\(\begin{array}{l} = \frac{7}{5} + \frac{{18}}{5}\\ = \frac{{25}}{5} = 5\end{array}\)
b) \(\left( {\frac{{ - 5}}{9}} \right).\frac{3}{{11}} + \left( {\frac{{ - 4}}{9}} \right).\frac{3}{{11}}\)
\(\begin{array}{l} = \frac{3}{{11}}.\left[ {\left( {\frac{{ - 5}}{9}} \right) + \left( {\frac{{ - 4}}{9}} \right)} \right]\\ = \frac{3}{{11}}.\left( { - 1} \right) = \frac{{ - 3}}{{11}}\end{array}\)
c) \(2023 - {\left( {\frac{1}{3}} \right)^2}{.3^2}\)
\(\begin{array}{l} = 2023 - \frac{1}{9}.9\\ = 2023 - 1 = 2022\end{array}\)
d) \(\frac{{{5^{16}}{{.27}^7}}}{{{{125}^5}{{.9}^{11}}}}\)\( = \frac{{{5^{16}}.{{({3^3})}^7}}}{{{{({5^3})}^5}.{{({3^2})}^{11}}}}\)\( = \frac{{{5^{16}}{{.3}^{21}}}}{{{5^{15}}{{.3}^{22}}}}\)\( = \frac{5}{3}\)
Sử dụng quy tắc chuyển vế và thực hiện phép tính với số hữu tỉ để tìm x.
a) \(x - \frac{2}{3} = \frac{{ - 1}}{3}\)
\(\begin{array}{l}x = \left( {\frac{{ - 1}}{3}} \right) + \frac{2}{3}\\x = \frac{1}{3}\end{array}\)
Vậy \(x = \frac{1}{3}\).
b) \(\frac{7}{3}.x + \frac{4}{7} = \frac{{ - 3}}{7}\)
\(\begin{array}{l}\frac{7}{3}.x = \left( {\frac{{ - 3}}{7}} \right) - \frac{4}{7}\\\frac{7}{3}.x = - 1\\x = - 1:\frac{7}{3}\\x = - \frac{3}{7}\end{array}\)
Vậy \(x = - \frac{3}{7}\).
Dựa vào công thức tính thể tích của hình hộp chữ nhật suy ra chiều cao.
Vì \(V = h.S\) nên \(h = \frac{V}{S}\) (với V là thể tích; h là chiều cao, S là diện tích đáy).
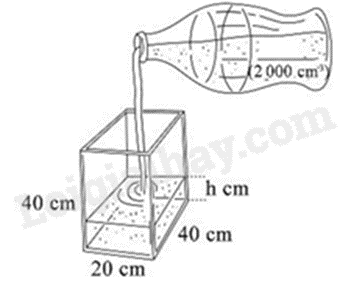
Thể tích phần nước sau khi rót hết vào bể chính là thể tích của chai nước. Do đó thể tích phần nước trong bể là \(2000c{m^3}\).
Vì phần nước trong bể cũng là một hình hộp chữ nhật với kích thước đáy là kích thước bể nên thể tích phần nước trong bể là:
\(V = h.S\) hay \(2000 = h.20.40\)
Do đó chiều cao mực nước sau khi rót hết một chai nước vào bể là:
\(h = \frac{{2000}}{{20.40}} = 2,5\left( {cm} \right)\)
Vậy chiều cao mực nước sau khi rót hết một chai nước vào bể là \(2,5cm\).
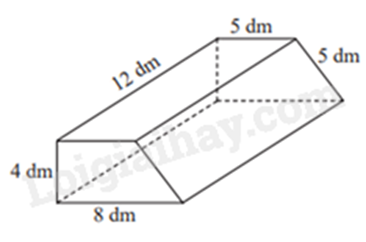
a) Sử dụng công thức tính diện tích xung quanh của hình lăng trụ: S xq = C đáy . h.
b) Tính diện tích hai đáy.
Tính diện tích cần sơn (gồm hai mặt đáy và 3 mặt bên (trừ mặt bên dưới)).
Chi phí bằng diện tích cần sơn . 25 nghìn đồng.
a) Diện tích xung quanh chiếc hộp là:
S xq = C đáy . h = (4 + 5 + 5 + 8) . 12 = 264 (dm 2 )
Diện tích 2 đáy là:
S 2đáy = (5 + 8). 4 : 2 . 2 = 52 (dm 2 )
Các mặt cần sơn gồm hai mặt đáy và 3 mặt bên (trừ mặt bên dưới) nên diện tích phần cần sơn là:
264 + 52 – 8.12 = 220 (dm 2 ) = 2,2 (m 2 )
Do đó chi phí để sơn là:
2,2 . 25 = 55 (nghìn đồng).
a) Dựa vào kiến thức về hai góc đối đỉnh.
b) Dựa vào kiến thức về hai góc đối đỉnh và hai góc kề nhau để tìm x.
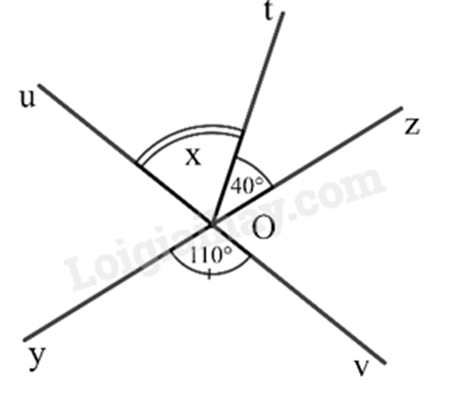
a) Góc đối đỉnh với góc \(\widehat {yOv}\) là góc \(\widehat {uOz}\)
b) Vì hai góc \(\widehat {yOv}\) và \(\widehat {uOz}\) là hai góc đối đỉnh nên \(\widehat {yOv}{\rm{ = }}\widehat {uOz} = 110^\circ \)
Ta có: Vì \(\widehat {uOt}\) kề với \(\widehat {tOz}\) nên \(\widehat {uOt}{\rm{ + }}\widehat {tOz} = \widehat {uOz}\)
hay \(\widehat {uOt} + 40^\circ = 110^\circ \)
Suy ra \(\widehat {uOt} = 110^\circ - 40^\circ = 70^\circ \)
Dựa vào đề bài để viết phép tính.
Giá của chiếc máy tính bảng sau 2 đợt giảm là
\(20000000.(100\% - 10\% ).(100\% - 8\% ) = 16560000\) (đồng)