Đề thi giữa kì 1 Toán 7 - Đề số 12
Phần trắc nghiệm (3 điểm) Chọn câu trả lời đúng trong mỗi câu sau:
Đề bài
Trong các số \( - \frac{1}{3};\,\,0;\,\,1,5;\,\, - \left( {\frac{{ - 1}}{2}} \right)\), các số hữu tỉ âm là:
-
A.
\(1,5;\,\,0\).
-
B.
\( - \frac{1}{3}\).
-
C.
\( - \frac{1}{3};\,\, - \left( {\frac{{ - 1}}{2}} \right)\).
-
D.
\( - \left( {\frac{{ - 1}}{2}} \right)\).
Số đối của số hữu tỉ \( - 2\frac{3}{5}\) dưới dạng phân số là:
-
A.
\(2\frac{3}{5}\).
-
B.
\(\frac{{ - 13}}{5}\).
-
C.
\(\frac{{13}}{5}\).
-
D.
\( - 2,6\).
Chọn khẳng định đúng trong các khẳng định sau.
-
A.
Số hữu tỉ âm nhỏ hơn số hữu tỉ dương.
-
B.
Số 0 là số hữu tỉ dương.
-
C.
Số nguyên âm không phải là số hữu tỉ âm.
-
D.
Tập hợp \(\mathbb{Q}\) gồm các số hữu tỉ dương và các số hữu tỉ âm.
Cho số hữu tỉ \(x\). Chọn khẳng định đúng?
-
A.
\({x^m}.{x^n} = {x^{m.n}}\).
-
B.
\({\left( {x.y} \right)^n} = {x^n} + {y^n}\).
-
C.
\({x^m}:{x^n} = {x^{m - n}} \left( {x \ne 0;\,\,m \ge n} \right)\).
-
D.
\({\left( {{x^m}} \right)^n} = {x^{m + n}}\).
Cho \(A = \frac{3}{{n - 2}}\). Tìm điều kiện của số nguyên n để A là một số hữu tỉ.
-
A.
\(n > 2\).
-
B.
\(n < 2\).
-
C.
\(n = 2\).
-
D.
\(n \ne 2\).
-
A.
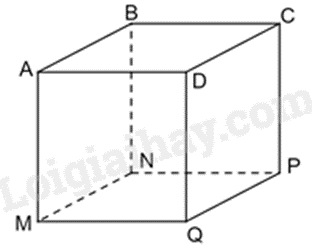
Bốn đường chéo \(AP,\,BP,\,CM,\,DB\).
-
B.
Ba góc vuông ở đỉnh A: góc \(DAB\), góc \(DAM\), góc \(MAB\).
-
C.
\(AM = AB = AD = AC\).
-
D.
Bốn mặt bên là \(ABCD\), \(MNPQ\), \(AMNB\),\(BNPC\).
-
A.
Hình 1 và Hình 2.
-
B.
Hình 2 và Hình 3.
-
C.
Hình 3.
-
D.
Tất cả các hình trên.
Diện tích xung quanh của hình hộp chữ nhật có độ dài hai đáy là \(6\,cm;\,\,8\,cm\) và chiều cao \(10\,cm\) là:
-
A.
\(6.8.10\,\left( {c{m^2}} \right)\).
-
B.
\(\left( {6 + 8} \right).10\,\left( {c{m^2}} \right)\).
-
C.
\(6 + 8 + 10\,\left( {c{m^2}} \right)\).
-
D.
\(2.\left( {6 + 8} \right).10\,\left( {c{m^2}} \right)\).
-
A.
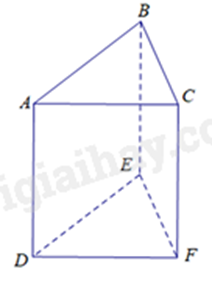
\(ABC;{\rm{ }}DEF\).
-
B.
\(ABC;{\rm{ }}DEF;{\rm{ }}ACFD\).
-
C.
\(ABED;{\rm{ }}BCFE\).
-
D.
\(ABED;{\rm{ }}BCFE;{\rm{ }}ACFD\).
Cho hình lăng trụ đứng có chu vi đáy, diện tích đáy và chiều cao lần lượt là \(C,S,h\). Khẳng định đúng là
-
A.
\({S_{xq}} = C.h\).
-
B.
\(V = C.S\).
-
C.
\(V = C.h\).
-
D.
\({S_{xq}} = \frac{V}{h}\).
-
A.
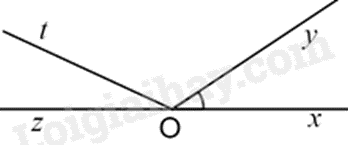
\(\widehat {zOy}\).
-
B.
\(\widehat {tOy}\).
-
C.
\(\widehat {tOz}\).
-
D.
\(\widehat {xOt}\).
-
A.
\(140^\circ \).
-
B.
\(90^\circ \).
-
C.
\(50^\circ \).
-
D.
\(40^\circ \).
Lời giải và đáp án
Trong các số \( - \frac{1}{3};\,\,0;\,\,1,5;\,\, - \left( {\frac{{ - 1}}{2}} \right)\), các số hữu tỉ âm là:
-
A.
\(1,5;\,\,0\).
-
B.
\( - \frac{1}{3}\).
-
C.
\( - \frac{1}{3};\,\, - \left( {\frac{{ - 1}}{2}} \right)\).
-
D.
\( - \left( {\frac{{ - 1}}{2}} \right)\).
Đáp án : B
Số hữu tỉ âm là các số hữu tỉ nhỏ hơn 0.
Có 1 số hữu tỉ âm là: \( - \frac{1}{3}\).
Đáp án B.
Số đối của số hữu tỉ \( - 2\frac{3}{5}\) dưới dạng phân số là:
-
A.
\(2\frac{3}{5}\).
-
B.
\(\frac{{ - 13}}{5}\).
-
C.
\(\frac{{13}}{5}\).
-
D.
\( - 2,6\).
Đáp án : C
Số đối của số hữu tỉ a là – a.
Ta có: \( - 2\frac{3}{5} = - \frac{{13}}{5}\) nên số đối của \( - 2\frac{3}{5}\) là \( - \left( { - \frac{{13}}{5}} \right) = \frac{{13}}{5}\).
Đáp án C.
Chọn khẳng định đúng trong các khẳng định sau.
-
A.
Số hữu tỉ âm nhỏ hơn số hữu tỉ dương.
-
B.
Số 0 là số hữu tỉ dương.
-
C.
Số nguyên âm không phải là số hữu tỉ âm.
-
D.
Tập hợp \(\mathbb{Q}\) gồm các số hữu tỉ dương và các số hữu tỉ âm.
Đáp án : A
Dựa vào kiến thức về số hữu tỉ.
Số hữu tỉ âm nhỏ hơn số hữu tỉ dương nên A đúng.
Số 0 không phải số hữu tỉ âm cũng không phải số hữu tỉ dương nên B sai.
Số nguyên âm cũng là số hữu tỉ âm nên C sai.
Tập hợp \(\mathbb{Q}\) gồm các số hữu tỉ dương, các số hữu tỉ âm và số 0 nên D sai.
Đáp án A.
Cho số hữu tỉ \(x\). Chọn khẳng định đúng?
-
A.
\({x^m}.{x^n} = {x^{m.n}}\).
-
B.
\({\left( {x.y} \right)^n} = {x^n} + {y^n}\).
-
C.
\({x^m}:{x^n} = {x^{m - n}} \left( {x \ne 0;\,\,m \ge n} \right)\).
-
D.
\({\left( {{x^m}} \right)^n} = {x^{m + n}}\).
Đáp án : C
Dựa vào kiến thức về lũy thừa với số mũ tự nhiên.
Ta có:
+) \({x^m}.{x^n} = {x^{m + n}}\) nên A sai.
+) \({\left( {x.y} \right)^n} = {x^n}.{y^n}\) nên B sai.
+) \({x^m}:{x^n} = {x^{m - n}} \left( {x \ne 0;\,\,m \ge n} \right)\) nên khẳng định C đúng.
+) \({\left( {{x^m}} \right)^n} = {x^{m.n}}\) nên khẳng định D sai.
Đáp án C.
Cho \(A = \frac{3}{{n - 2}}\). Tìm điều kiện của số nguyên n để A là một số hữu tỉ.
-
A.
\(n > 2\).
-
B.
\(n < 2\).
-
C.
\(n = 2\).
-
D.
\(n \ne 2\).
Đáp án : D
Một số là số hữu tỉ thì mẫu số của số đó khác 0.
Để A là một số hữu tỉ thì \(n - 2 \ne 0\) suy ra \(n \ne 2\).
Đáp án D.
-
A.
Bốn đường chéo \(AP,\,BP,\,CM,\,DB\).
-
B.
Ba góc vuông ở đỉnh A: góc \(DAB\), góc \(DAM\), góc \(MAB\).
-
C.
\(AM = AB = AD = AC\).
-
D.
Bốn mặt bên là \(ABCD\), \(MNPQ\), \(AMNB\),\(BNPC\).
Đáp án : B
Dựa vào đặc điểm của hình lập phương.
Các đường chéo của hình lập phương là \(AP,BQ,CM,DN\) nên A sai.
Ba góc vuông ở đỉnh A là: góc \(DAB\), góc \(DAM\), góc \(MAB\) nên B đúng.
Vì ABCD.MNPQ là hình lập phương nên \(AM = AB = AD\). AC là đường chéo của ABCD nên AC không bằng AM. Do đó khẳng định C sai.
Bốn mặt bên của hình lập phương là ABNM, BCPN, CDQP, ADQM nên khẳng định D sai.
Đáp án B.
-
A.
Hình 1 và Hình 2.
-
B.
Hình 2 và Hình 3.
-
C.
Hình 3.
-
D.
Tất cả các hình trên.
Đáp án : D
Dựa vào kiến thức về hình lăng trụ đứng.
Hình hộp chữ nhật và hình lập phương cũng là hình lăng trụ đứng tứ giác.
Cả 3 hình đều là hình lăng trụ đứng, trong đó Hình 1 và Hình 2 là hình lăng trụ đứng tứ giác (hình hộp chữ nhật và hình lập phương cũng là hình lăng trụ đứng tứ giác); Hình 3 là hình lăng trụ đứng tam giác.
Đáp án D.
Diện tích xung quanh của hình hộp chữ nhật có độ dài hai đáy là \(6\,cm;\,\,8\,cm\) và chiều cao \(10\,cm\) là:
-
A.
\(6.8.10\,\left( {c{m^2}} \right)\).
-
B.
\(\left( {6 + 8} \right).10\,\left( {c{m^2}} \right)\).
-
C.
\(6 + 8 + 10\,\left( {c{m^2}} \right)\).
-
D.
\(2.\left( {6 + 8} \right).10\,\left( {c{m^2}} \right)\).
Đáp án : D
Sử dụng công thức tính diện tích xung quanh của hình hộp chữ nhật:
S xq = C đáy . h
Diện tích xung quanh của hình hộp chữ nhật là:
\({S_{xq}} = 2(6 + 8).10\left( {c{m^2}} \right)\).
Đáp án D.
-
A.
\(ABC;{\rm{ }}DEF\).
-
B.
\(ABC;{\rm{ }}DEF;{\rm{ }}ACFD\).
-
C.
\(ABED;{\rm{ }}BCFE\).
-
D.
\(ABED;{\rm{ }}BCFE;{\rm{ }}ACFD\).
Đáp án : D
Dựa vào kiến thức về hình lăng trụ tam giác.
Các mặt bên của lăng trụ là: ABED, BCFE, ACFD.
Đáp án D.
Cho hình lăng trụ đứng có chu vi đáy, diện tích đáy và chiều cao lần lượt là \(C,S,h\). Khẳng định đúng là
-
A.
\({S_{xq}} = C.h\).
-
B.
\(V = C.S\).
-
C.
\(V = C.h\).
-
D.
\({S_{xq}} = \frac{V}{h}\).
Đáp án : A
Dựa vào công thức tính diện tích xung quanh và thể tích của hình lăng trụ.
Công thức tính diện tích xung quanh của hình lăng trụ đứng là: \({S_{xq}} = C.h\).
Thể tích của hình lăng trụ đứng là: \(V = S.h\).
Vậy đáp án đúng là A.
Đáp án A.
-
A.
\(\widehat {zOy}\).
-
B.
\(\widehat {tOy}\).
-
C.
\(\widehat {tOz}\).
-
D.
\(\widehat {xOt}\).
Đáp án : A
Dựa vào kiến thức về hai góc kề bù.
Góc kề bù với góc \(xOy\) là \(\widehat {zOy}\).
Đáp án A.
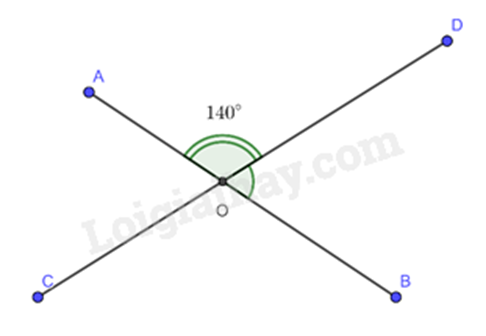
-
A.
\(140^\circ \).
-
B.
\(90^\circ \).
-
C.
\(50^\circ \).
-
D.
\(40^\circ \).
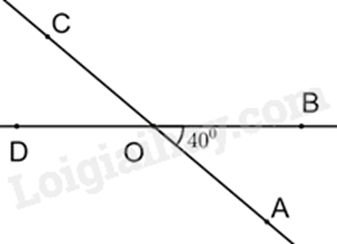
Đáp án : D
Dựa vào kiến thức về hai góc đối đỉnh: hai góc đối đỉnh thì bằng nhau.
Vì \(\widehat {COD}\) và \(\widehat {AOB}\) là hai góc đối đỉnh nên \(\widehat {COD} = \widehat {AOB} = 40^\circ \).
Đáp án D.
Dựa vào quy tắc tính với số hữu tỉ, lũy thừa với số mũ tự nhiên.
a) \(\frac{7}{3} + \frac{{ - 8}}{{12}} + \frac{5}{4}\)
= \(\frac{{28}}{{12}} + \frac{{ - 8}}{{12}} + \frac{{15}}{{12}}\)
= \(\frac{{35}}{{12}}.\)
b) \({\left( {\frac{{ - 2}}{3}} \right)^2}.\frac{{67}}{4} + \frac{{ - 7}}{4}.{\left( {\frac{{ - 2}}{3}} \right)^2}\)
\( = {\left( {\frac{{ - 2}}{3}} \right)^2}.\left( {\frac{{67}}{4} + \frac{{ - 7}}{4}} \right)\)
\( = \frac{4}{9}.\frac{{60}}{4}\)\( = \frac{{60}}{9} = \frac{{20}}{3}.\)
c) \(\left( {\frac{6}{{23}} - \frac{6}{{33}}} \right) - \left( {\frac{{27}}{{33}} - \frac{{17}}{{23}}} \right) + 2\frac{4}{7}\)
\( = \frac{6}{{23}} - \frac{6}{{33}} - \frac{{27}}{{33}} + \frac{{17}}{{23}} + 2\frac{4}{7}\)
\( = \left( {\frac{6}{{23}} + \frac{{17}}{{23}}} \right) + \left( {\frac{{ - 6}}{{33}} + \frac{{ - 27}}{{33}}} \right) + 2\frac{4}{7}\)
\( = 1 + \left( { - 1} \right) + 2\frac{4}{7}\)\( = 2\frac{4}{7}\)
a), b) Chuyển vế để tìm x.
c) Với \({A^2} = {B^2}\), ta chia hai trường hợp: TH1: A = B; TH2: A = - B.
a) \(\frac{6}{7} - x = \frac{{12}}{{28}}\)
\(x = \frac{6}{7} - \frac{{12}}{{28}}\)
\(x = \frac{{24}}{{28}} - \frac{{12}}{{28}}\)
\(x = \frac{{12}}{{28}} = \frac{3}{7}\)
Vậy \(x = \frac{3}{7}\)
b) \(\frac{{ - 5}}{3} + \frac{7}{{10}}x = 0,2\)
\(\frac{7}{{10}}x = \frac{1}{5} + \frac{5}{3}\)
\(\frac{7}{{10}}x = \frac{3}{{15}} + \frac{{25}}{{15}} = \frac{{28}}{{15}}\)
\(x = \frac{{28}}{{15}}:\frac{7}{{10}}\)
\(x = \frac{8}{3}\)
Vậy \(x = \frac{8}{3}\)
c) \({\left( {2x + 6} \right)^2} = \frac{{81}}{{25}}\)
\({\left( {2x + 6} \right)^2} = {\left( {\frac{9}{5}} \right)^2} = {\left( {\frac{{ - 9}}{5}} \right)^2}.\)
* TH1: \(2x + 6 = \frac{9}{5}\)
\(2x = \frac{9}{5} - 6\)
\(2x = \frac{{ - 21}}{5}\)
\(x = \frac{{ - 21}}{5}:2\)
\(x = \frac{{ - 21}}{{10}}.\)
* TH2: \(2x + 6 = \frac{{ - 9}}{5}\)
\(2x = \frac{{ - 9}}{5} - 6\)
\(2x = \frac{{ - 39}}{5}\)
\(x = \frac{{ - 39}}{5}:2\)
\(x = \frac{{ - 39}}{{10}}.\)
Vậy \(x \in \left\{ {\frac{{ - 39}}{{10}};\frac{{ - 21}}{{10}}} \right\}\).
Sử dụng kiến thức hai góc kề bù: Hai góc kề bù thì tổng của chúng bằng \(180^\circ \).
Vì \(\widehat {AOD}\) và \(\widehat {DOB}\) là 2 góc kề bù nên \(\widehat {AOD} + \widehat {DOB} = 180^\circ \)
\(140^\circ + \widehat {DOB} = 180^\circ \)
\(\widehat {DOB} = 180^\circ - 140^\circ \)
\(\widehat {DOB} = 40^\circ .\)
Vậy \(\widehat {DOB} = 40^\circ .\)
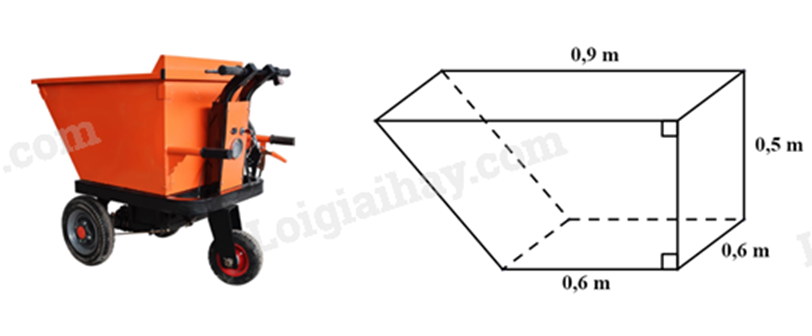
Sử dụng công thức tính thể tích hình lăng trụ đứng tứ giác.
Tính thể tích cát của mỗi chuyến xe.
Từ đó tính số chuyến xe ít nhất để vận chuyển hết cát.
Thể tích của thùng xe là:
\(\frac{{\left( {0,9 + 0,6} \right).0,5}}{2}.0,6 = 0,225\,\left( {{m^3}} \right)\)
Thể tích cát của mỗi chuyến xe là:
\(0,225.96\% = 0,216\,\left( {{m^3}} \right)\)
Ta có: \(54:0,216\, = 250\).
Vậy cần ít nhất 250 chuyến xe để có thể vận chuyển hết \(54\,{m^3}\) cát.
Tính giá vốn của 50 chiếc điện thoại.
Tính số tiền bán được của 40 chiếc điện thoại.
Tính giá tiền của một chiếc điện thoại khi bán với giá bằng \(120\% \)giá vốn.
Tính số tiền còn thiếu để được lãi \(70000000\) đồng từ lô hàng trên.
Tính giá tiền của một chiếc điện thoại sau khi giảm giá.
Tính phần trăm giá tiền của chiếc điện thoại sau khi giá so với giá bán trước đó.
Giá vốn của 50 chiếc điện thoại là:
\(50.10\,000\,000 = 500\,000\,000\) (đồng)
Số tiền bán được của 40 chiếc điện thoại là:
\(40.10\,000\,000.120\% = 480\,000\,000\) (đồng)
Giá tiền của một chiếc điện thoại khi bán với giá bằng \(120\% \) giá vốn là:
\(10\,000\,000.120\% = 12\,000\,000\) (đồng)
Số tiền còn thiếu để được lãi \(70\,000\,000\) đồng từ lô hàng trên là:
\(500\,000\,000 + 70\,000\,000 - 480\,000\,000 = 90\,000\,000\) (đồng)
Giá tiền của một chiếc điện thoại sau khi giảm giá là:
\(90\,000\,000:10 = 9\,000\,000\) (đồng)
Phần trăm giá tiền của chiếc điện thoại sau khi giá so với giá bán trước đó là:
\(\frac{{9\,000\,000}}{{12\,000\,000}} = 0,75 = 75\% \)
Vậy để lãi được \(70\,000\,000\) đồng từ lô hàng trên thì cửa hàng đã giảm \(100\% - 75\% = 25\% \) so với giá bán trước đó.