Đề thi giữa kì 2 Toán 6 Kết nối tri thức - Đề số 7 — Không quảng cáo

Dựa vào khái niệm về phân số.

\(\frac{{0,25}}{{ - 3}}\) không phải phân số vì \(0,25 \notin \mathbb{Z}\).

\(\frac{5}{0}\) không phải phân số vì 0 nằm ở mẫu.

\(\frac{{6,23}}{{7,4}}\) không phải phân số vì \(6,23;7,4 \notin \mathbb{Z}\).

\(\frac{4}{7}\) là phân số vì \(4;7 \in \mathbb{Z};7 \ne 0\).

Đáp án A.

Số đối của phân số \(\frac{a}{b}\) là phân số \( - \frac{a}{b}\).

Số đối của phân số \( - \frac{{16}}{{25}}\) là \(\frac{{16}}{{25}}\).

Đáp án A.

Sử dụng quy tắc nhân cả tử và mẫu của một phân số: Nếu ta nhân cả tử và mẫu của một phân số với cùng 1 số nguyên khác 0 thì ta được một phân số bằng phân số đã cho.

Ta có: \(\frac{3}{4} = \frac{{3.2}}{{4.2}} = \frac{6}{8}\) nên phân số \(\frac{6}{8} = \frac{3}{4}\).

Đáp án C.

Hai phân số \(\frac{a}{b} = \frac{c}{d}\) nếu ad = bc.

Ta có: \(\frac{2}{{ - 3}} = \frac{6}{{ - y}}\) nên

\(\begin{array}{l}2.\left( { - y} \right) = 6.\left( { - 3} \right)\\ - 2y =  - 18\\y = 9\end{array}\)

Đáp án D.

Dựa vào quy tắc làm tròn số.

Số \(3,148\) được làm tròn đến hàng phần chục là 3,1.

Đáp án B.

Dựa vào kiến thức về số thập phân.

Phân số \(\frac{{ - 31}}{{10}}\) được viết dưới dạng số thập phân là -3,1.

Đáp án D.

Muốn tìm giá trị a% của số b, ta tính: \(b.a\%  = b.\frac{a}{{100}}\).

25% của 20 là: \(20.25\%  = 20.\frac{{25}}{{100}} = 20.\frac{1}{4} = 5\).

Đáp án B.

Dựa vào quy tắc cộng, trừ số thập phân.

Ta có:

\(\begin{array}{l}1,3 + 3,4 - 4,7 + 5,6 - 4,3\\ = 1,3 + \left( {3,4 + 5,6} \right) - \left( {4,7 + 4,3} \right)\\ = 1,3 + 9 - 9\\ = 1,3\end{array}\)

Đáp án A.

Quan sát hình vẽ để trả lời.

Có 4 giao điểm tạo bởi 4 đường thẳng trong hình trên.

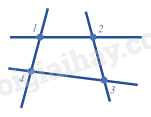
Đáp án D.

Dựa vào kiến thức về điểm và đường thẳng.

Qua hai điểm phân biệt ta chỉ vẽ được 1 đường thẳng nên A đúng.

Đáp án A.

Dựa vào kiến thức về tia.

Hai tia OA và OB là hai tia đối nhau.

Đáp án A.

Dựa vào kiến thức về đoạn thẳng.

Có 6 đoạn thẳng trong hình vẽ, đó là: KJ, KL, KN, JL, JN, LN.

Đáp án D.

Dựa vào các quy tắc tính với phân số và số thập phân.

a) A = \(\frac{1}{2}\) + \(\frac{1}{3}\) = \(\frac{3}{6} + \frac{2}{6} = \frac{5}{6}\)

b) B = 6,3 + (-6,3) + 4,9 = [6,3 + (-6,3)] + 4,9 = 0 + 4,9 = 4,9

c) \(C = \frac{{ - 3}}{7} + \frac{5}{{14}} - \frac{4}{7} + \frac{3}{{12}} + \frac{9}{{14}}\)\( = \left( {\frac{{ - 3}}{7} - \frac{4}{7}} \right) + \left( {\frac{5}{{14}} + \frac{9}{{14}}} \right) + \frac{3}{{12}}\) \( = - 1 + 1 + \frac{3}{{12}}\) \( = \frac{3}{{12}}\) = \(\frac{1}{4}\)

Dựa vào quy tắc tính với phân số và số thập phân để tìm x.

a) x - 5,01 = 7,02 - 2.1,5

x - 5,01 = 4,02

x = 4,02 + 5,01

x = 9,03

Vậy \(x = 9,03\)

b) \(\frac{1}{5} - \left( {\frac{2}{3} - x} \right) = \frac{{ - 3}}{5}\)

\(\frac{2}{3} - x = \frac{1}{5} - \frac{{ - 3}}{5}\)

\(x = \frac{2}{3} - \frac{4}{5}\)

Vậy x = \(\frac{{ - 2}}{{15}}\)

Sử dụng các phép tính với phân số và tỉ số phần trăm để tìm tính chiều dài đám đất, diện tích trồng cây, diên tích ao cá.

Sử dụng công thức tính diện tích hình chữ nhật để tính diện tích đám đất.

Tính diện tích ao bằng bao nhiêu phần trăm diện tích cả đám đất bằng công thức:

Diện tích ao : diện tích cả đám đất . 100.

Chiều dài đám đất là:  \(60.\frac{4}{3} = 80\)(m)

Diện tích đám đất là:  \(60.80 = 4800\)(m ² )

Diện tích trồng cây là: \(4800.\frac{7}{{12}} = 2800\)(m ² )

Diện tích đất còn lại sau khi trồng cây là: \(4800 - 2800 = 2000\)(m)

Diện tích ao cá:     \(2000.30\%  = 600\)(m ² )

Diện tích ao bằng: \(600:4880 = {\rm{ }}0,125{\rm{ }} = 12,5\% \).

Vẽ hình theo yêu cầu đề bài.

a) Sử dụng tính chất của trung điểm để tìm OM, ON.

b) Vì O nằm giữa MN nên MN = OM + ON.

a) Do \(M\) là trung điểm của \(OA\) nên ta có:

\(OM = MA = \frac{{OA}}{2} = \frac{6}{2} = 3(cm)\)

Do \(N\) là trung điểm của \(OB\) nên ta có:

\(ON = NB = \frac{{OB}}{2} = \frac{3}{2} = 1,5(cm)\)

b) Vì điểm \(O\) nằm giữa hai điểm \(M,N\) nên ta có: \(MN = OM + ON\)

Suy ra \(MN = 3 + 1,5 = 4,5(cm)\)

Vậy \({\rm{MN  =  4,5 cm}}\).

a) Nhân cả tử và mẫu của các phân số trong A với 2.

Rút 2 ra ngoài, biến đổi các phân số \(\frac{1}{{a\left( {a + 1} \right)}}\) thành \(\frac{1}{a} - \frac{1}{{a + 1}}\) (vì \(\frac{1}{{a\left( {a + 1} \right)}} = \frac{1}{a} - \frac{1}{{a + 1}}\))

Tính A.

b) Để chứng minh phân số tổi giản, ta chứng minh ƯCLN của tử số và mẫu số là 1.

a) Ta có \(A = \frac{1}{3} + \frac{1}{6} + \frac{1}{{10}} + \frac{1}{{15}} + ... + \frac{1}{{45}} = \frac{2}{6} + \frac{2}{{12}} + \frac{2}{{20}} + \frac{2}{{30}} + ... + \frac{2}{{90}}\)

\(\begin{array}{l} = 2\left( {\frac{1}{{2.3}} + \frac{1}{{3.4}} + \frac{1}{{4.5}} + \frac{1}{{5.6}} + ... + \frac{1}{{9.10}}} \right)\\ = 2\left( {\frac{1}{2} - \frac{1}{3} + \frac{1}{3} - \frac{1}{4} + \frac{1}{4} - \frac{1}{5} + \frac{1}{5} - \frac{1}{6} + ... + \frac{1}{9} - \frac{1}{{10}}} \right)\end{array}\)

\( = 2\left( {\frac{1}{2} - \frac{1}{{10}}} \right) = 2.\frac{4}{{10}} = \frac{4}{5}\).

Vậy \(A = \frac{4}{5}.\)

b) Gọi ƯCLN\(\left( {n - 1\,;\,n - 2} \right) = d\) suy ra \(n - 1 \vdots d\,\,\,,\,\,n - 2 \vdots d\)

suy ra \(\left( {n - 1} \right) - \left( {n - 2} \right) \vdots d\)suy ra \(1 \vdots d \Rightarrow d = 1\) với mọi \(n\)

Vậy với mọi \(n \in {\rm Z}\) thì \(M = \frac{{n - 1}}{{n - 2}}\) là phân số tối giản.