Đề thi học kì 1 Toán 7 Cánh diều - Đề số 13
Phần trắc nghiệm (3 điểm)
Đề bài
Căn bậc hai số học của 36 là:
-
A.
\(\sqrt 6 \) .
-
B.
6.
-
C.
– 6.
-
D.
–\(\sqrt 6 \).
Khẳng định nào sau đây đúng?
-
A.
\( - 1,(3)\, \notin \,\,\mathbb{R}\) .
-
B.
\(3,5\, \in \,\,{\rm{I}}\).
-
C.
\(\pi \, \in \,\,\mathbb{R}\).
-
D.
\(\sqrt {11} \, \notin \,\,{\rm{I}}\).
Cho \(\left| x \right|\) = 9 thì giá trị của x là:
-
A.
x = 9 hoặc x = –9 .
-
B.
x = 3.
-
C.
x = 3 hoặc x = – 3.
-
D.
x = –9.
Hình hộp chữ nhật \({\rm{ABCD}}{\rm{.}}\,{\rm{A'B'C'D'}}\)có \({\rm{AD}}\,{\rm{ = }}\,7{\rm{cm}}\). Khẳng định nào sau đây đúng?
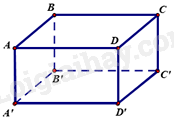
-
A.
\({\rm{A'B'}} = 7\,{\rm{cm}}\) . .
-
B.
\({\rm{B'C'}} = 7\,{\rm{cm}}\)
-
C.
\({\rm{CC'}} = 7{\rm{cm}}\).
-
D.
\({\rm{BD'}} = 7{\rm{cm}}\).
-
A.
Hình thoi.
-
B.
Hình bình hành.
-
C.
Hình thang cân.
-
D.
Hình chữ nhật.
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Hãy chọn khẳng định luôn luôn đúng trong các khẳng định sau:
-
A.
a.b = c.d.
-
B.
a.d = c.b.
-
C.
a + b = c + d.
-
D.
a + c = b + d.
-
A.
Hình trụ đứng tam giác.
-
B.
Hình lăng trụ đứng lục giác.
-
C.
Hình trụ.
-
D.
Hình lập phương.
Cho x và y là hai đại lượng tỉ lệ nghịch, biết khi x = 6 thì y = 3. Tìm hệ số tỉ lệ nghịch của x đối với y là:
-
A.
18.
-
B.
9.
-
C.
3.
-
D.
2.
Trong các số sau, số nào biểu diễn số thập phân vô hạn tuần hoàn?
-
A.
\(\frac{1}{{10}}\).
-
B.
\(\frac{2}{5}\).
-
C.
\(\frac{7}{6}\).
-
D.
\(\sqrt {13} \).
-
A.
Ox.
-
B.
Oy.
-
C.
Ot.
-
D.
không có.
-
A.
60 0 .
-
B.
65 0 .
-
C.
115 0 .
-
D.
100 0 .
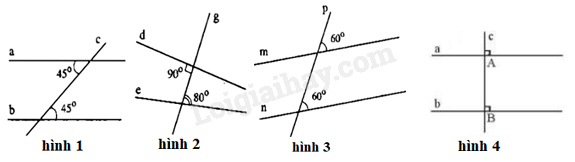
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Lời giải và đáp án
Căn bậc hai số học của 36 là:
-
A.
\(\sqrt 6 \) .
-
B.
6.
-
C.
– 6.
-
D.
–\(\sqrt 6 \).
Đáp án : B
Sử dụng kiến thức về căn bậc hai số học: Căn bậc hai số học của số a không âm là số x không âm sao cho \({x^2} = a\).
Căn bậc hai số học của 36 là \(\sqrt {36} = 6\).
Khẳng định nào sau đây đúng?
-
A.
\( - 1,(3)\, \notin \,\,\mathbb{R}\) .
-
B.
\(3,5\, \in \,\,{\rm{I}}\).
-
C.
\(\pi \, \in \,\,\mathbb{R}\).
-
D.
\(\sqrt {11} \, \notin \,\,{\rm{I}}\).
Đáp án : C
\(\mathbb{R}\) là tập hợp các số thực.
\(I\) là tập hợp các số vô tỉ.
\( - 1,\left( 3 \right)\) là số thực nên A sai.
\(3,5 = \frac{{35}}{{10}} = \frac{7}{2}\) là số hữu tỉ nên không phải là số vô tỉ, do đó \(3,5 \notin \,{\rm{I}}\) nên B sai.
\(\pi = 3,14...\) là số thực, \(\pi \, \in \,\,\mathbb{R}\) nên C đúng.
\(\sqrt {11} \) là số vô tỉ nên D sai.
Cho \(\left| x \right|\) = 9 thì giá trị của x là:
-
A.
x = 9 hoặc x = –9 .
-
B.
x = 3.
-
C.
x = 3 hoặc x = – 3.
-
D.
x = –9.
Đáp án : A
Dựa vào kiến thức về dấu giá trị tuyệt đối.
Ta có: \(\left| x \right| = 9\) thì x = 9 hoặc x = –9.
Hình hộp chữ nhật \({\rm{ABCD}}{\rm{.}}\,{\rm{A'B'C'D'}}\)có \({\rm{AD}}\,{\rm{ = }}\,7{\rm{cm}}\). Khẳng định nào sau đây đúng?

-
A.
\({\rm{A'B'}} = 7\,{\rm{cm}}\) . .
-
B.
\({\rm{B'C'}} = 7\,{\rm{cm}}\)
-
C.
\({\rm{CC'}} = 7{\rm{cm}}\).
-
D.
\({\rm{BD'}} = 7{\rm{cm}}\).
Đáp án : B
Dựa vào kiến thức về hình hộp chữ nhật.
Ta có: AD = A’D’ = B’C’ = BC = 7cm nên B đúng.
-
A.
Hình thoi.
-
B.
Hình bình hành.
-
C.
Hình thang cân.
-
D.
Hình chữ nhật.
Đáp án : D
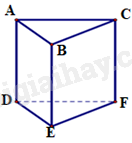
Hình lăng trụ đứng tam giác là hình hai mặt đáy là hình tam giác song song với nhau, ba mặt bên là các hình chữ nhật, các cạnh bên song song và bằng nhau.
Hình lăng trụ đứng tam giác ABC.DEF có các cạnh bên là các hình chữ nhật nên chọn đáp án D.
Cho tỉ lệ thức \(\frac{a}{b} = \frac{c}{d}\). Hãy chọn khẳng định luôn luôn đúng trong các khẳng định sau:
-
A.
a.b = c.d.
-
B.
a.d = c.b.
-
C.
a + b = c + d.
-
D.
a + c = b + d.
Đáp án : B
Sử dụng kiến thức về tỉ lệ thức.
Nếu \(\frac{a}{b} = \frac{c}{d}\) thì \(ad = cb\) nên B đúng.
-
A.
Hình trụ đứng tam giác.
-
B.
Hình lăng trụ đứng lục giác.
-
C.
Hình trụ.
-
D.
Hình lập phương.
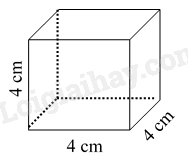
Đáp án : D
Dựa vào đặc điểm các hình đã học.
Hình lăng trụ đứng tứ giác bên có các cạnh bằng nhau và bằng 4cm nên hình bên là hình lập phương.
Cho x và y là hai đại lượng tỉ lệ nghịch, biết khi x = 6 thì y = 3. Tìm hệ số tỉ lệ nghịch của x đối với y là:
-
A.
18.
-
B.
9.
-
C.
3.
-
D.
2.
Đáp án : A
Dựa vào kiến thức về tỉ lệ nghịch: Hệ số tỉ lệ nghịch của x và y là x.y.
Vì x và y là hai đại lượng tỉ lệ nghịch nên hệ số tỉ lệ nghịch của x đối với y là x.y = 6.3 = 18.
Trong các số sau, số nào biểu diễn số thập phân vô hạn tuần hoàn?
-
A.
\(\frac{1}{{10}}\).
-
B.
\(\frac{2}{5}\).
-
C.
\(\frac{7}{6}\).
-
D.
\(\sqrt {13} \).
Đáp án : C
Các phân số tối giản với mẫu số dương mà mẫu có ước nguyên tố khác 2 và 5 đều viết được dưới dạng số thập phân vô hạn tuần hoàn.
\(\frac{1}{{10}}\) và \(\frac{2}{5}\) có mẫu chỉ có ước nguyên tố là 2 và 5 nên không biểu diễn số thập phân vô hạn tuần hoàn.
\(\frac{7}{6}\) mẫu số có ước là 2 và 3 nên biểu diễn số thập phân vô hạn tuần hoàn.
\(\sqrt {13} \) không viết được dưới dạng phân số nên không phải số thập phân vô hạn tuần hoàn.
-
A.
Ox.
-
B.
Oy.
-
C.
Ot.
-
D.
không có.
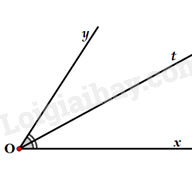
Đáp án : C
Dựa vào tính chất tia phân giác của một góc: \(Ot\) là tia phân giác của \(\widehat {xOy}\) nên \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}\widehat {xOy}\).
Vì \(\widehat {xOt} = \widehat {tOy}\) và Ot nằm trong góc xOy nên Ot là tia phân giác của góc xOy.
-
A.
60 0 .
-
B.
65 0 .
-
C.
115 0 .
-
D.
100 0 .
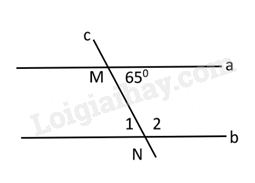
Đáp án : B
Dựa vào tính chất của hai đường thẳng song song: Hai đường thẳng song song với nhau thì hai góc so le trong bằng nhau.
Vì a // b nên \(\widehat {{N_1}} = \widehat {NMa} = {65^0}\) (2 góc so le trong).
-
A.
Hình 1.
-
B.
Hình 2.
-
C.
Hình 3.
-
D.
Hình 4.
Đáp án : B
Dựa vào dấu hiệu nhận biết hai đường thẳng song song.
Hình 1 có hai góc so le trong bằng nhau (= 45 0 ) nên hình 1 có hai đường thẳng song song.
Hình 2 hai góc so le trong không bằng nhau nên hình 2 không có hai đường thẳng song song.
Hình 3 có hai góc đồng vị bằng nhau (= 60 0 ) nên hình 3 có hai đường thẳng song song.
Hình 4 có hai góc đồng vị bằng nhau (= 90 0 ) nên hình 4 có hai đường thẳng song song.
Số đối của số a là – a.
- Số đối của \(\frac{{11}}{{29}}\) là \( - \,\,\frac{{11}}{{29}}\).
- Số đối của \( - \sqrt {97} \) là \( - \left( { - \sqrt {97} } \right) = \sqrt {97} \).
a) Nhóm nhân tử chung để tính.
b) Sử dụng quy tắc chuyển vế để tìm x.
a) \(\frac{7}{{10}} \cdot \frac{{15}}{{19}} + \frac{7}{{10}} \cdot \frac{4}{{19}}\)
\(\begin{array}{l} = \frac{7}{{10}}\left( {\frac{{15}}{{19}} + \frac{4}{{19}}} \right)\\ = \frac{7}{{10}}.1\\ = \frac{7}{{10}}\end{array}\)
b) \(0,8 - \left( {{\rm{x + }}\frac{3}{5}} \right) = \frac{1}{2}\)
\(\begin{array}{l}\frac{4}{5} - \left( {{\rm{x + }}\frac{3}{5}} \right) = \frac{1}{2}\\x + \frac{3}{5} = \frac{4}{5} - \frac{1}{2}\\x + \frac{3}{5} = \frac{3}{{10}}\\x = \frac{3}{{10}} - \frac{3}{5}\\x = \frac{{ - 3}}{{10}}\end{array}\)
Vậy \(x = \frac{{ - 3}}{{10}}\).
Thực hiện phép chia: 647 : 45.
Làm tròn kết quả lên để tính số ổ tô tối thiểu cần để chở hết số học sinh.
Ta có: 647 : 45 \( \approx \) 14,4
Vậy cần sử dụng tối thiểu 15 ô tô để chở hết số học sinh trên.
Sử dụng tính chất của dãy tỉ số bằng nhau.
Gọi số học sinh của 3 lớp 7A, 7B, 7C lần lượt là x , y , z ( x, y, z \( \in \)N*, học sinh)
Theo đề bài ta có:
\(\frac{x}{8} = \frac{y}{{10}} = \frac{z}{9}\) và x + y + z = 108
Theo tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{x}{8} = \frac{y}{{10}} = \frac{z}{9} = \frac{{x + y + z}}{{8 + 10 + 9}} = \frac{{108}}{{27}} = 4\)
Suy ra
\(\frac{x}{8} = 4 \Rightarrow x = 32\) ; \(\frac{y}{{10}} = 4 \Rightarrow y = 40\); \(\frac{z}{9} = 4 \Rightarrow x = 36\)
Vậy số học sinh tham gia về nguồn của 3 lớp 7A,7B, 7C lần lượt là 32, 40, 36 học sinh.
- Sử dụng công thức tính thể tích hình hộp chữ nhật để tính: thể tích con đường, thể tích xe chở cát.
- Tính số xe chở cát.
- Tính số tiền cát phải trả.
Thể tích con đường dẫn từ đường nhựa vào nhà là: 24.2,5.1 = 60 (m 3 ).
Thể tích xe tải chở cát là: 3.2,5.1 = 7,5 (m 3 ).
Số lượng xe chở cát cần để làm xong con đường là: 60 : 7,5 = 8 (xe).
Tổng số tiền cát phải trả là: 8 . 1 200 000 = 9 600 000 (đồng).
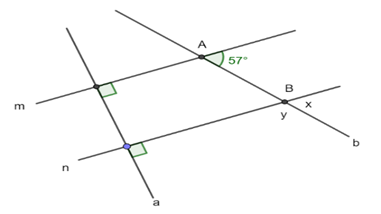
a) Chứng minh 2 góc đồng vị bằng nhau nên m // n.
b) Sử dụng tính chất của hai đường thẳng song song và tính chất hai góc kề bù để tính số đo x, y.
a) Ta có m \( \bot \) a (gt) và n \( \bot \) a (gt) \( \Rightarrow \) m // n.
b) Vì m // n nên ta có \({\rm{x = }}\widehat {{\rm{ A}}}{\rm{ = 5}}{{\rm{7}}^{\rm{0}}}\,\,\)(2 góc đồng vị)
\( \Rightarrow \) y = 180 0 – x = 180 0 – 57 0 = 123 0 (2 góc kề bù)
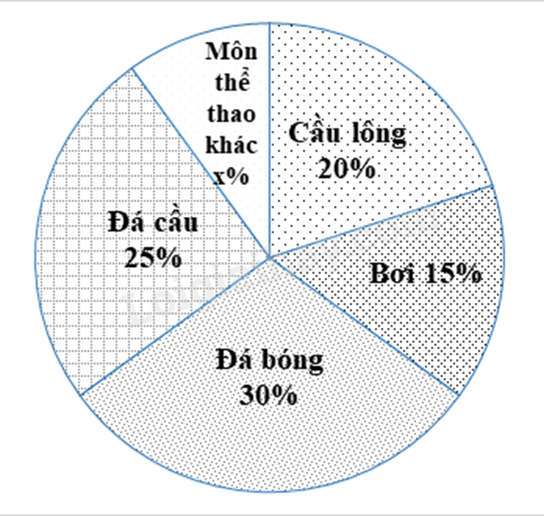
Vì tổng số phần trăm học sinh là 100% nên số phần trăm học sinh yêu thích môn thể thao khác bằng 100% - số phần trăm học sinh thích các môn thể thao còn lại (đá bóng, đá cầu, cầu lông, bơi).
Số phần trăm học sinh yêu thích các môn thể thao khác là:
100% – (20% + 15% + 30% + 25%) = 10% (số học sinh trường)
Sử dụng cách làm tròn số.
- Dân số nam: 47 881 061 $\approx $ 47 881 000 người.
- Dân số nữ: 48 327 923 $\approx $ 48 328 000 người.
a) Dữ liệu định tính là dữ liệu không phải là số.
Dữ liệu định lượng là dữ liệu số.
b) Nếu tổng số bạn nam tham gia khảo sát bằng số học sinh lớp 7C thì dữ liệu trên đại diện được mức độ yêu thích đối với việc đọc sách trong thư viện của các bạn học sinh lớp 7C.
a)
- Dữ liệu định tính là: sở thích (không thích, thích, rất thích, không quan tâm)
- Dữ liệu định lượng là: số bạn nam (5; 7; 6; 4)
b) Số bạn nam tham gia khảo sát là: 5 + 7 + 6 + 4 = 22 (học sinh). Vì số học sinh lớp 7C là 50 học sinh nên dữ liệu trên chưa có đại diện được cho mức độ yêu thích đối với việc đọc sách trong thư viện của các bạn học sinh lớp 7C vì đối tượng khảo sát còn thiếu các bạn nữ.
- Tính thời gian người đó chạy bộ từ nhà đến công viên.
- Thời gian chạy bộ từ công viên đến quán cà phê.
- Tính tốc độ của người đó từ công viên đến quán cà phê.
Thời gian người đó chạy từ nhà đến công viên là: 874,8: 97,2 = 9 (phút)
Thời gian người đó chạy từ công viên đến quán cà phê là: 34,6 – (9 + 10) = 15,6 (phút)
Quãng đường người đó chạy bộ từ công viên đến quán cà phê là: 874,8 – 360 = 514,8 (m)
Tốc độ chạy bộ của người đó từ công viên đến quán cà phê là: 514,8 : 15,6 = 33 (m/phút)