Đề thi học kì 1 Toán 8 - Đề số 3 - Chân trời sáng tạo
Phần trắc nghiệm (3 điểm) Câu 1: Kết quả của phép tính (xy + 5)(xy – 1) là:
Đề bài
Kết quả của phép tính (xy + 5)(xy – 1) là:
-
A.
xy 2 + 4xy – 5 .
-
B.
x 2 y 2 + 4xy – 5 .
-
C.
x 2 – 2xy – 1 .
-
D.
x 2 + 2xy + 5 .
Giá trị của biểu thức \(5{x^2} - \left[ {4{x^2} - 3x\left( {x - 2} \right)} \right]\) tại x = \(\frac{1}{2}\) là:
-
A.
– 3
-
B.
3
-
C.
– 2
-
D.
2
Cho phân thức \(\frac{{x + y}}{{x - y}}\):
Điều kiện xác định của phân thức \(\frac{{x + y}}{{x - y}}\) là:
-
A.
\(x \ne y\).
-
B.
\(x \ne - y\).
-
C.
\(x \ne 1\).
-
D.
\(x \ne 0;y \ne 0\).
Phân thức đối của phân thức \(\frac{{x + y}}{{x - y}}\) là:
-
A.
\(\frac{{x + y}}{{x - y}}\).
-
B.
\(\frac{{y + x}}{{x - y}}\).
-
C.
\(\frac{{x + y}}{{y - x}}\).
-
D.
\(\frac{{x - y}}{{x + y}}\).
Rút gọn biểu thức \(\frac{{{x^3} - 3{x^2} + 3x - 1}}{{x - 1}}\) được kết quả nào sau đây?
-
A.
\({x^2} - 3x - 1\).
-
B.
\({x^2} + 3x - 1\).
-
C.
\({x^2} - 2x - 1\).
-
D.
\({x^2} - 2x + 1\).
Hình nào sau đây là hình vuông ?
-
A.
Hình thang cân có một góc vuông.
-
B.
Hình thoi có một góc vuông.
-
C.
Tứ giác có 3 góc vuông.
-
D.
Hình bình hành có một góc vuông.
AM là trung tuyến của tam giác vuông ABC (\(\widehat A = {90^0};M \in BC\)) thì:
-
A.
AC = 2.AM
-
B.
CB = 2.AM
-
C.
BA = 2.AM
-
D.
AM = 2.BC
Hình bình hành ABCD có \(\widehat A = 2\widehat B\). Số đo góc D là:
-
A.
60 0 .
-
B.
120 0 .
-
C.
30 0 .
-
D.
45 0 .
-
A.
1 hình.
-
B.
2 hình.
-
C.
3 hình.
-
D.
4 hình.
Cho hình chóp tam giác đều có độ dài cạnh đáy là 5cm, độ dài trung đoạn của hình chóp là 6cm. Diện tích xung quanh của hình chóp tam giác đều đó là :
-
A.
\(40c{m^2}\).
-
B.
\(36c{m^2}\).
-
C.
\(45c{m^2}\).
-
D.
\(50c{m^2}\).
Hình chóp tứ giác đều S.ABCD có các mặt bên là những tam giác đều AB = 8cm, O là trung điểm của AC. Độ dài đoạn SO là:
-
A.
\(8\sqrt 2 \)cm.
-
B.
6cm.
-
C.
\(\sqrt {32} \)cm.
-
D.
4cm.
Cho bảng thống kê tỉ lệ các loại mẫu vật trong bảo tàng sinh vật của môi trường đại học về những lớp động vật có xương sống: Cá, Lưỡng cư, Bò sát, Chim, Động vật có vú.

Giá trị chưa hợp lí trong bảng dữ liệu là:
-
A.
Dữ liệu về tên các lớp động vật.
-
B.
Dữ liệu tỉ lệ mẫu vật.
-
C.
A & B đều đúng.
-
D.
A & B đều sai.
Thống kê số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong các năm 2015; 2018; 2019; 2020 . (đơn vi: triệu lượt người)

Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2015 là
-
A.
36,4.
-
B.
53,7.
-
C.
58,5.
-
D.
19,1.
Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2020 là
-
A.
36,4.
-
B.
53,7.
-
C.
58,5
-
D.
19,1.
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong bảng thống kê trên?
-
A.
Biểu đồ tranh.
-
B.
Biểu đồ cột kép.
-
C.
Biểu đồ đoạn thẳng.
-
D.
A; B; C đều sai.
Biểu đồ cột kép ở hình bên biểu diễn trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022.
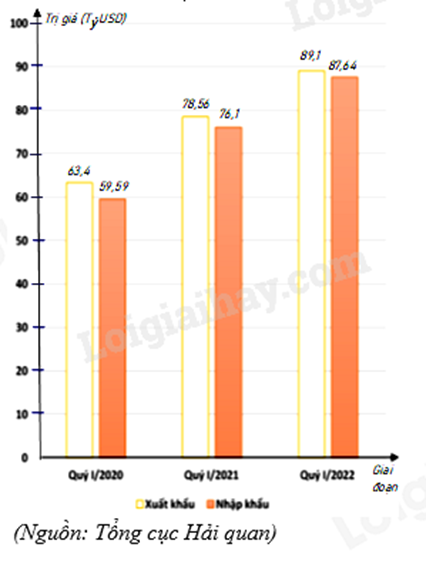
a) Lập bảng thống kê trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022: đơn vị (tỷ USD) theo mẫu sau:
|
Giai đoạn |
Quý I/2020 |
Quý I/2021 |
Quý I/2022 |
|
Xuất khẩu |
? |
? |
? |
|
Nhập khẩu |
? |
? |
? |
b) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
c) Tổng trị giá nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
d) Trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 giảm bao nhiêu phần trăm so với quý I năm 2021 (làm tròn kết quả đến hàng phần mười) ?
Lời giải và đáp án
Kết quả của phép tính (xy + 5)(xy – 1) là:
-
A.
xy 2 + 4xy – 5 .
-
B.
x 2 y 2 + 4xy – 5 .
-
C.
x 2 – 2xy – 1 .
-
D.
x 2 + 2xy + 5 .
Đáp án : B
Sử dụng quy tắc nhân hai đa thức.
Ta có:
\(\begin{array}{l}(xy + 5)(xy - 1)\\ = {x^2}{y^2} + 5xy - xy - 5\\ = {x^2}{y^2} + 4xy - 5\end{array}\)
Giá trị của biểu thức \(5{x^2} - \left[ {4{x^2} - 3x\left( {x - 2} \right)} \right]\) tại x = \(\frac{1}{2}\) là:
-
A.
– 3
-
B.
3
-
C.
– 2
-
D.
2
Đáp án : C
Rút gọn biểu thức.
Thay x = \(\frac{1}{2}\) vào biểu thức để tính giá trị.
Ta có:
\(\begin{array}{l}5{x^2} - \left[ {4{x^2} - 3x\left( {x - 2} \right)} \right]\\ = 5{x^2} - \left( {4{x^2} - 3{x^2} + 6x} \right)\\ = 5{x^2} - 4{x^2} + 3{x^2} - 6x\\ = 4{x^2} - 6x\end{array}\)
Thay x = \(\frac{1}{2}\) vào biểu thức, ta được:\(4{\left( {\frac{1}{2}} \right)^2} - 6.\left( {\frac{1}{2}} \right) = 1 - 3 = - 2\).
Cho phân thức \(\frac{{x + y}}{{x - y}}\):
Điều kiện xác định của phân thức \(\frac{{x + y}}{{x - y}}\) là:
-
A.
\(x \ne y\).
-
B.
\(x \ne - y\).
-
C.
\(x \ne 1\).
-
D.
\(x \ne 0;y \ne 0\).
Đáp án: A
Sử dụng kiến thức về phân thức đại số.
Điều kiện xác định của phân thức \(\frac{{x + y}}{{x - y}}\) là \(x - y \ne 0 \Leftrightarrow x \ne y\).
Phân thức đối của phân thức \(\frac{{x + y}}{{x - y}}\) là:
-
A.
\(\frac{{x + y}}{{x - y}}\).
-
B.
\(\frac{{y + x}}{{x - y}}\).
-
C.
\(\frac{{x + y}}{{y - x}}\).
-
D.
\(\frac{{x - y}}{{x + y}}\).
Đáp án: C
Sử dụng kiến thức về phân thức đại số.
Phân thức đối của phân thức \(\frac{{x + y}}{{x - y}}\) là \( - \left( {\frac{{x + y}}{{x - y}}} \right) = \frac{{x + y}}{{ - \left( {x - y} \right)}} = \frac{{x + y}}{{y - x}}\).
Rút gọn biểu thức \(\frac{{{x^3} - 3{x^2} + 3x - 1}}{{x - 1}}\) được kết quả nào sau đây?
-
A.
\({x^2} - 3x - 1\).
-
B.
\({x^2} + 3x - 1\).
-
C.
\({x^2} - 2x - 1\).
-
D.
\({x^2} - 2x + 1\).
Đáp án : D
Sử dụng kiến thức về phân thức đại số.
Ta có:
\(\frac{{{x^3} - 3{x^2} + 3x - 1}}{{x - 1}} = \frac{{{{\left( {x - 1} \right)}^3}}}{{x - 1}} = {\left( {x - 1} \right)^2} = {x^2} - 2x + 1\)
Hình nào sau đây là hình vuông ?
-
A.
Hình thang cân có một góc vuông.
-
B.
Hình thoi có một góc vuông.
-
C.
Tứ giác có 3 góc vuông.
-
D.
Hình bình hành có một góc vuông.
Đáp án : B
Sử dụng dấu hiệu nhận biết hình vuông.
Hình thang cân có một góc vuông là hình chữ nhật nên A sai .
Hình thoi có một góc vuông là hình vuông nên B đúng .
Tứ giác có 3 góc vuông là hình chữ nhật nên C sai .
Hình bình hành có một góc vuông là hình chữ nhật nên D sai .
AM là trung tuyến của tam giác vuông ABC (\(\widehat A = {90^0};M \in BC\)) thì:
-
A.
AC = 2.AM
-
B.
CB = 2.AM
-
C.
BA = 2.AM
-
D.
AM = 2.BC
Đáp án : B
Dựa vào kiến thức về đường trung tuyến ứng với cạnh huyền trong tam giác vuông.
Ta có tam giác ABC vuông tại A và AM là đường trung tuyến (\(M \in BC\)) nên AM chính là đường trung tuyến ứng với cạnh huyền của tam giác vuông ABC. Khi đó: AM = \(\frac{1}{2}\)BC hay BC = 2AM.
Hình bình hành ABCD có \(\widehat A = 2\widehat B\). Số đo góc D là:
-
A.
60 0 .
-
B.
120 0 .
-
C.
30 0 .
-
D.
45 0 .
Đáp án : A
Dựa vào đặc điểm của hình bình hành.
vuông.
Ta có: \(\widehat A + \widehat B = {180^0}\) (hai góc kề một cạnh bù nhau). Mà \(\widehat A = 2\widehat B\) nên:
\(\begin{array}{l}2\widehat B + \widehat B = {180^0}\\3\widehat B = {180^0}\\\widehat B = {180^0}:3 = {60^0}\end{array}\)
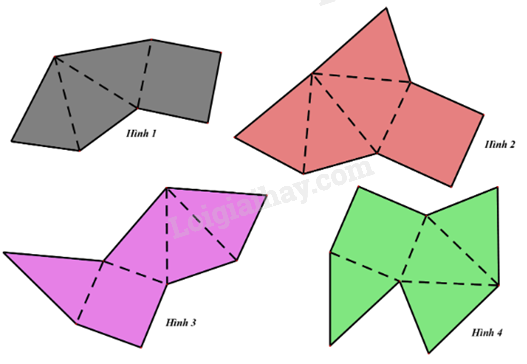
-
A.
1 hình.
-
B.
2 hình.
-
C.
3 hình.
-
D.
4 hình.
Đáp án : B
Sử dụng kiến thức về hình chóp tứ giác đều.
Hình 2 và hình 3 có thể gấp lại thành hình chóp tứ giác đều.
Cho hình chóp tam giác đều có độ dài cạnh đáy là 5cm, độ dài trung đoạn của hình chóp là 6cm. Diện tích xung quanh của hình chóp tam giác đều đó là :
-
A.
\(40c{m^2}\).
-
B.
\(36c{m^2}\).
-
C.
\(45c{m^2}\).
-
D.
\(50c{m^2}\).
Đáp án : C
Sử dụng công thức tính diện tích xung quanh của hình chóp tam giác đều.
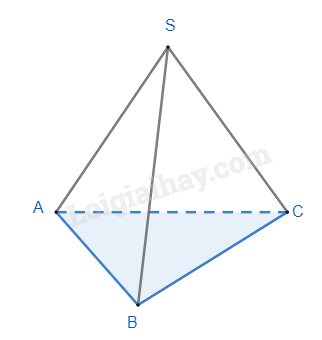
Diện tích xung quanh của hình chóp là:
\({S_{xq}} = \frac{{5.3}}{2}.6 = 45\left( {c{m^2}} \right)\)
Hình chóp tứ giác đều S.ABCD có các mặt bên là những tam giác đều AB = 8cm, O là trung điểm của AC. Độ dài đoạn SO là:
-
A.
\(8\sqrt 2 \)cm.
-
B.
6cm.
-
C.
\(\sqrt {32} \)cm.
-
D.
4cm.
Đáp án : C
Sử dụng công thức tính thể tích hình chóp tứ giác đều.
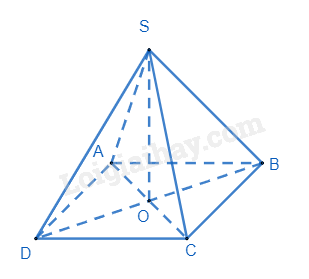
Hình chóp tứ giác đều S.ABCD có đáy là hình vuông, O là trung điểm của AC nên SO là đường cao của hình chóp S.ABCD.
Xét tam giác ABC vuông tại B, áp dụng định lí Pythagore, ta có:
\(\begin{array}{l}A{C^2} = A{B^2} + B{C^2} = {8^2} + {8^2} = 128\\ \Rightarrow AC = \sqrt {128} = 8\sqrt 2 \\ \Rightarrow AO = \frac{{8\sqrt 2 }}{2} = 4\sqrt 2 \end{array}\)
Vì tam giác SAB đều nên SA = AB = 8cm. Xét tam giác SAO vuông tại O, áp dụng định lí Pythagore, ta có:
\(\begin{array}{l}S{O^2} = S{A^2} - A{O^2} = {8^2} - {\left( {4\sqrt 2 } \right)^2} = 32\\ \Rightarrow SO = \sqrt {32} \end{array}\)
Cho bảng thống kê tỉ lệ các loại mẫu vật trong bảo tàng sinh vật của môi trường đại học về những lớp động vật có xương sống: Cá, Lưỡng cư, Bò sát, Chim, Động vật có vú.

Giá trị chưa hợp lí trong bảng dữ liệu là:
-
A.
Dữ liệu về tên các lớp động vật.
-
B.
Dữ liệu tỉ lệ mẫu vật.
-
C.
A & B đều đúng.
-
D.
A & B đều sai.
Đáp án : B
Quan sát bảng thống kê để xác định.
Trong bảng thống kê trên, ta thấy tổng tỉ lệ mẫu vật bằng 15% + 10% + 20% + 25% + 30% = 100% nên dữ liệu về tổng tỉ lệ mẫu vật chưa chính xác. Vậy dữ liệu tỉ lệ mẫu vật chưa hợp lí.
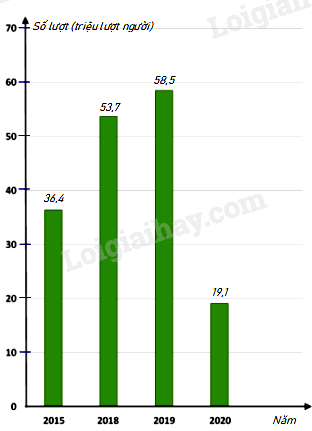
Thống kê số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong các năm 2015; 2018; 2019; 2020 . (đơn vi: triệu lượt người)

Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2015 là
-
A.
36,4.
-
B.
53,7.
-
C.
58,5.
-
D.
19,1.
Đáp án: A
Quan sát bảng thống kê để trả lời câu hỏi.
Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2015 là 36,4 triệu lượt người.
Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2020 là
-
A.
36,4.
-
B.
53,7.
-
C.
58,5
-
D.
19,1.
Đáp án: D
Quan sát bảng thống kê để trả lời câu hỏi.
Số lượt hành khách vận chuyển bằng đường bộ ở Khánh Hòa trong năm 2020 là 19,1 triệu lượt người.
Lựa chọn biểu đồ nào để biểu diễn các dữ liệu thống kê có trong bảng thống kê trên?
-
A.
Biểu đồ tranh.
-
B.
Biểu đồ cột kép.
-
C.
Biểu đồ đoạn thẳng.
-
D.
A; B; C đều sai.
Đáp án: D
Quan sát bảng thống kê để trả lời câu hỏi.
Dữ liệu trên nên được biểu diễn bởi biểu đồ cột.
a) Để A có nghĩa thì mẫu thức phải khác 0.
b) Sử dụng các phép tính với phân thức để rút gọn.
c) Để A nguyên thì tử thức phải chia hết cho mẫu thức.
a) Điều kiện để A có nghĩa là: \(\left\{ \begin{array}{l}x - 2 \ne 0\\x + 2 \ne 0\\{x^2} - 4 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne 2\\x \ne - 2\end{array} \right.\)
b) Ta có:
\(\begin{array}{l}A = \left( {\frac{1}{{x - 2}} + \frac{x}{{x + 2}} - \frac{{x + 1}}{{{x^2} - 4}}} \right):\left( {1 + \frac{1}{{x - 2}}} \right)\\ = \left[ {\frac{{x + 2}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} + \frac{{x\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} - \frac{{x + 1}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}} \right]:\left( {\frac{{x - 2 + 1}}{{x - 2}}} \right)\\ = \left[ {\frac{{x + 2 + {x^2} - 2x - x - 1}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}} \right]:\left( {\frac{{x - 1}}{{x - 2}}} \right)\\ = \frac{{{x^2} - 2x + 1}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}.\frac{{x - 2}}{{x - 1}}\\ = \frac{{{{\left( {x - 1} \right)}^2}\left( {x - 2} \right)}}{{\left( {x - 2} \right)\left( {x + 2} \right)\left( {x - 1} \right)}}\\ = \frac{{x - 1}}{{x + 2}}\end{array}\)
Vậy \(A = \frac{{x - 1}}{{x + 2}}\).
c) Ta có: \(A = \frac{{x - 1}}{{x + 2}} = \frac{{x + 2 - 3}}{{x + 2}} = 1 - \frac{3}{{x + 2}}\). Để A là số nguyên thì \(\frac{3}{{x + 2}}\) nguyên, hay \(\left( {x + 2} \right) \in U\left( 3 \right) = \left\{ { \pm 1; \pm 3} \right\}\).
Ta có bảng giá trị sau:
|
x + 2 |
-1 |
1 |
-3 |
3 |
|
x |
-3 (TM) |
-1 (TM) |
-5 (TM) |
1 (TM) |
|
\(A = \frac{{x - 1}}{{x + 2}}\) |
4 |
-2 |
2 |
0 |
Vậy để A nguyên thì \(x \in \left\{ { - 3; - 1; - 5;1} \right\}\)
Sử dụng các phép tính và hằng đẳng thức đáng nhớ.
a) 6x 2 – (2x – 3)(3x + 2) = 1
6x 2 – (6x 2 – 9x + 4x – 6) = 1
6x 2 – 6x 2 + 9x – 4x + 6 = 1
5x + 6 = 1
5x = -5
x = -1
Vậy x = -1.2
b) (x + 1) 3 – (x – 1)(x 2 + x + 1) – 2 = 0
(x 3 + 3x 2 + 3x + 1) – (x 3 – 1) – 2 = 0
x 3 + 3x 2 + 3x + 1 – x 3 + 1 – 2 = 0
3x 2 + 3x = 0
3x(x + 1) = 0
\(\begin{array}{l}\left[ \begin{array}{l}x = 0\\x + 1 = 0\end{array} \right.\\\left[ \begin{array}{l}x = 0\\x = - 1\end{array} \right.\end{array}\)
Vậy x = 0 hoặc x = -1.
Biểu đồ cột kép ở hình bên biểu diễn trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022.

a) Lập bảng thống kê trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022: đơn vị (tỷ USD) theo mẫu sau:
|
Giai đoạn |
Quý I/2020 |
Quý I/2021 |
Quý I/2022 |
|
Xuất khẩu |
? |
? |
? |
|
Nhập khẩu |
? |
? |
? |
b) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
c) Tổng trị giá nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là bao nhiêu tỷ USD ?
d) Trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 giảm bao nhiêu phần trăm so với quý I năm 2021 (làm tròn kết quả đến hàng phần mười) ?
Dựa vào bảng dữ liệu để trả lời.
a) Bảng thống kê trị giá xuất khẩu, nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022: đơn vị (tỷ USD)
|
Giai đoạn |
Quý I/2020 |
Quý I/2021 |
Quý I/2022 |
|
Xuất khẩu |
63,4 |
78,56 |
89,1 |
|
Nhập khẩu |
59,59 |
76,1 |
87,64 |
b) Tổng trị giá xuất khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là:
63,4 + 78,56 + 89,1 = 231,06 (tỷ USD)
c) Tổng trị giá nhập khẩu hàng hóa của nước ta trong quý I của giai đoạn 2020 - 2022 là
59,59 + 76,1 + 87,64 = 223,33 (tỷ USD)
d) Tỉ số phần trăm trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 và quý I năm 2021 là: \(\frac{{63,4}}{{78,56}}.100\% = 80,7\% \)
Trị giá xuất khẩu hàng hóa của nước ta trong quý I năm 2020 giảm 100 % - 80,7 % = 19,3 % so với quý I năm 2021.
1. Dựa vào định lí Pythagore để tính chiều cao của tấm kính.
2.
a) Chứng minh tứ giác AICD; BCDI có cặp cạnh đối song song và bằng nhau nên là hình bình hành.
b) Dựa vào tính chất hai đường thẳng song song để chứng minh \(\widehat {DIA} = \widehat {ECD}\).
Dựa vào tính chất hình bình hành để chứng minh AD = DE.
c) \(\widehat A = \widehat D = {90^0}\) và AD = CD nên hình bình hành AICD trở thành hình vuông. Sử dụng tính chất của hình vuông và hai đường thẳng song song để chứng minh \(BC \bot AC\).
1.
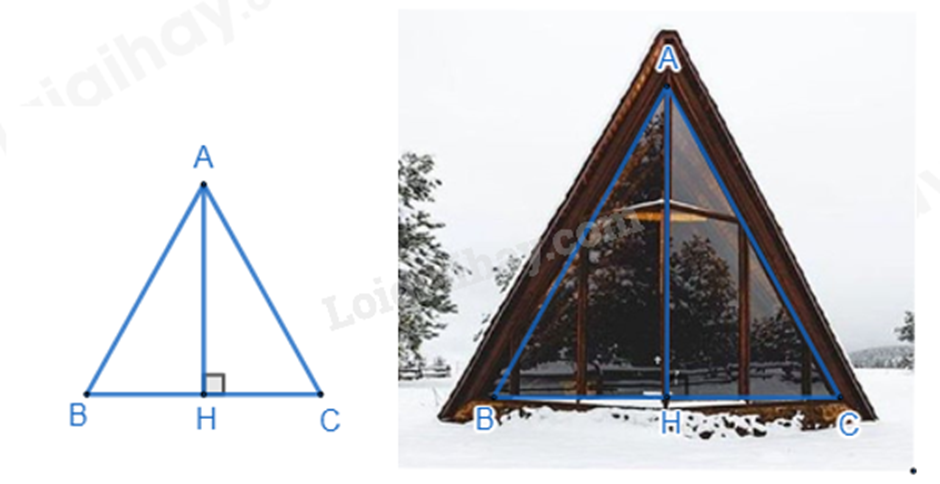
Gọi tam giác ABC là tam giác biểu thị tấm kính tam giác cân.
Kẻ \(AH \bot BC\) (H \( \in \) BC). Vì tam giác ABC cân tại A nên AH vừa là đường cao vừa là đường trung tuyến của tam giác ABC. Khi đó H là trung điểm của BC suy ra \(BH = \frac{1}{2}BC = \frac{1}{2}.8 = 4(m)\).
Áp dụng định lí Pythagore vào tam giác vuông AHB, ta có:
\(\begin{array}{l}A{H^2} = A{B^2} - B{H^2} = {10^2} - {4^2} = 84\\AH = \sqrt {84} \approx 9,2(m)\end{array}\)
Vậy chiều cao của tấm kính tam giác cân này xấp xỉ 9,2m.
2.
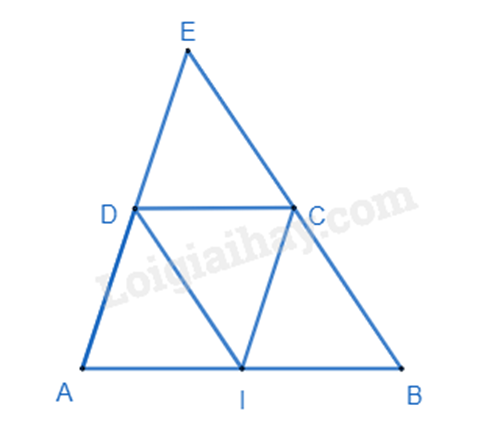
a) Ta có I là trung điểm của AB nên \(AI = IB = \frac{1}{2}AB\). Mà CD = \(\frac{1}{2}\)AB suy ra AI = IB = CD.
Xét tứ giác AICD có:
AI // CD (I \( \in \) AB)
AI = CD (cmt)
=> AICD là hình bình hành. (đpcm)
Xét tứ giác BCDI có:
BI // CD (I \( \in \) AB)
BI = CD (cmt)
=> BCDI là hình bình hành. (đpcm)
b) BCDI là hình bình hành nên BC // DI => \(\widehat {DIA} = \widehat {CBI}\) (hai góc đồng vị).
BI // CD nên \(\widehat {CBI} = \widehat {ECD}\) (hai góc đồng vị).
=> \(\widehat {DIA} = \widehat {ECD}\) (đpcm).
AICD là hình bình hành nên CI // AD và CI = AD. (1)
Xét tứ giác CEDI có:
CI // DE (CI // AD)
DI // CE (DI // BC)
=> CEDI là hình bình hành => CI = DE (hai cạnh tương ứng) (2)
Từ (1) và (2) suy ra AD = DE. (đpcm)
c) Vì \(\widehat A = \widehat D = {90^0}\)và AD = CD nên hình bình hành AICD trở thành hình vuông. Khi đó AC \( \bot \) DI.
Mà DI // BC nên AC \( \bot \) BC. (đpcm)