Đề thi học kì 1 Toán 8 - Đề số 2 - Chân trời sáng tạo
Phần trắc nghiệm (3 điểm) Câu 1: Thu gọn đa thức $2{{x}^{4}}y-4{{y}^{5}}+5{{x}^{4}}y-7{{y}^{5}}+{{x}^{2}}{{y}^{2}}-2{{x}^{4}}y$ ta được:
Đề bài
Thu gọn đa thức \(2{x^4}y - 4{y^5} + 5{x^4}y - 7{y^5} + {x^2}{y^2} - 2{x^4}y\) ta được:
-
A.
\(5{x^4}y + 11{y^5} + {x^2}{y^2}\).
-
B.
\(9{x^4}y - 11{y^5} + {x^2}{y^2}\).
-
C.
\( - 5{x^4}y - 11{y^5} + {x^2}{y^2}\).
-
D.
\(5{x^4}y - 11{y^5} + {x^2}{y^2}\).
Đa thức \({{\mathop{\rm x}\nolimits} ^5} + 4{x^3} - 6{x^2}\) chia hết cho đơn thức nào?
-
A.
4xy
-
B.
6x 3
-
C.
x 5
-
D.
4x 2
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
a. \(\frac{{{x^3} + 6{x^2} + 12x + 8}}{{x + 2}} = \)
b. Phân thức nghịch đảo của phân thức \(\frac{{x + y}}{{x - y}}\)
c. Phân thức đối của phân thức \(\frac{3}{{x - y}}\)
1. \(\frac{{x - y}}{{x + y}}\)
2. \(\frac{{ - 3}}{{x - y}}\)
3. x 2 + 4x + 4
Hình thang cân là hình thang
-
A.
có hai cạnh bên bằng nhau.
-
B.
có hai cạnh đáy bằng nhau.
-
C.
có hai góc kề một cạnh bên bù nhau.
-
D.
có hai góc kề một đáy bằng nhau.
Cho tam giác ABC, qua điểm D thuộc cạnh BC, kẻ các đường thẳng song song với AB và AC, cắt AC và AB theo thứ tự ở E và F. Tam giác ABC cần thêm điều kiện gì thì AEDF là chữ nhật?
-
A.
cân tại A.
-
B.
vuông tại A.
-
C.
vuông cân tại A.
-
D.
\(\widehat A = {60^0}\).
Cho tam giác ABC vuông tại A có AB = \(\frac{1}{2}\)BC, đường trung tuyến AM. Tam giác ABM là tam giác gì?
-
A.
vuông tại A.
-
B.
cân tại M.
-
C.
đều.
-
D.
cân tại B.
Cho hình chóp tam giác đều có độ dài cạnh bên bằng 4 cm và độ dài cạnh đáy bằng 3cm như hình bên dưới, hình nào là hình khai triển của hình chóp tam giác đều đã cho?
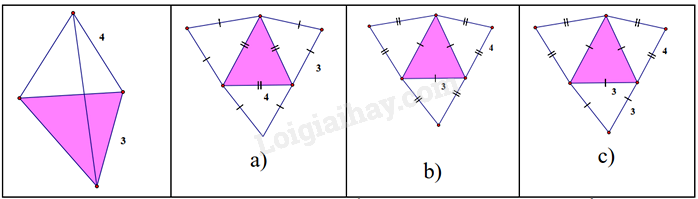
-
A.
Hình a).
-
B.
Hình b).
-
C.
Hình c).
-
D.
Không có hình nào.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3cm, chiều cao của hình chóp là h = 2cm. Thể tích của hình chóp đã cho là :
-
A.
6 cm \(^3\).
-
B.
18 cm \(^3\).
-
C.
12 cm \(^3\).
-
D.
9 cm \(^3\).
Hai đường chéo hình thoi có độ dài 8cm và 10cm. Cạnh của hình thoi có độ dài là:
-
A.
\(6cm\).
-
B.
\(\sqrt {41} cm\).
-
C.
\(\sqrt {164} cm\).
-
D.
\(9cm\).
Một số con vật sống trên cạn: Cá voi, chó, mèo , bò. Trong các dữ liệu trên, dữ liệu chưa hợp lí là:
-
A.
Cá voi.
-
B.
Chó.
-
C.
Mèo.
-
D.
Bò.
Trong cuộc khảo sát tìm hiểu về cách học của học sinh khối 8 được kết quả như sau:

Có 50 % học sinh học qua đọc, viết.
Có 35 % học sinh học qua nghe
Có 10 % học sinh học qua vận động.
Có 5 % học sinh học qua quan sát.
Khẳng định nào sau đây là đúng?
-
A.
Kết quả thu thập trên là dữ liệu không phải là số.
-
B.
Kết quả thu thập trên là số liệu.
-
C.
Kết quả trên gồm cả dữ liệu không phải là số và số liệu.
-
D.
Kết quả trên dữ liệu phần trăm là dữ liệu không phải là số.
Biểu đồ đoạn thẳng biểu diễn vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta qua các năm 2015; 2017; 2018; 2019; 2020. (đơn vị: nghìn tỷ đồng)
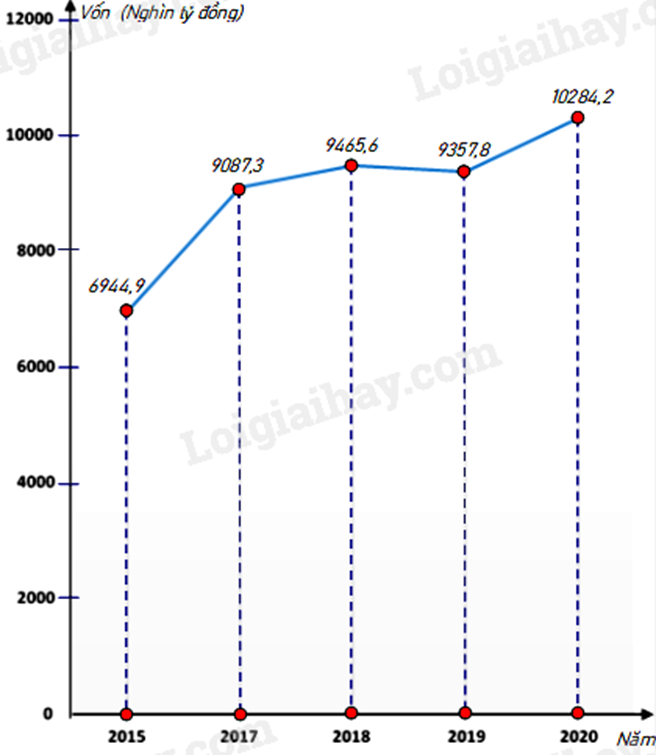
(Nguồn: Niên giám thống kê 2021)
a) Lập bảng thống kê vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta qua các năm 2015; 2017; 2018; 2019; 2020 theo mẫu sau:
|
Năm |
2015 |
2017 |
2018 |
2019 |
2020 |
|
Vốn (nghìn tỷ đồng) |
? |
? |
? |
? |
? |
b) Năm nào vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta là nhiều nhất? ít nhất?
c) Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng bao nhiêu phần trăm so năm 2015 (làm tròn kết quả đến hàng phần mười) ?
d) Năm 2017 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước giảm bao nhiêu phần trăm so năm 2019 (làm tròn kết quả đến hàng phần mười) ?
Lời giải và đáp án
Thu gọn đa thức \(2{x^4}y - 4{y^5} + 5{x^4}y - 7{y^5} + {x^2}{y^2} - 2{x^4}y\) ta được:
-
A.
\(5{x^4}y + 11{y^5} + {x^2}{y^2}\).
-
B.
\(9{x^4}y - 11{y^5} + {x^2}{y^2}\).
-
C.
\( - 5{x^4}y - 11{y^5} + {x^2}{y^2}\).
-
D.
\(5{x^4}y - 11{y^5} + {x^2}{y^2}\).
Đáp án : D
Sử dụng quy tắc tính với đa thức.
Ta có:
\(\begin{array}{l}2{x^4}y - 4{y^5} + 5{x^4}y - 7{y^5} + {x^2}{y^2} - 2{x^4}y\\ = \left( {2{x^4}y + 5{x^4}y - 2{x^4}y} \right) + \left( { - 4{y^5} - 7{y^5}} \right) + {x^2}{y^2}\\ = 5{x^4}y - 11{y^5} + {x^2}{y^2}\end{array}\)
Đa thức \({{\mathop{\rm x}\nolimits} ^5} + 4{x^3} - 6{x^2}\) chia hết cho đơn thức nào?
-
A.
4xy
-
B.
6x 3
-
C.
x 5
-
D.
4x 2
Đáp án : D
Dựa vào quy tắc chia đa thức cho đơn thức.
Đa thức chia hết cho một đơn thức nếu các hạng tử của đa thức đó chia hết cho đơn thức.
Vì vậy bậc của các biến đơn thức phải không lớn hơn bậc của các biến trong đa thức.
Đa thức \({{\mathop{\rm x}\nolimits} ^5} + 4{x^3} - 6{x^2}\) là đa thức biến x với bậc nhỏ nhất của biến x là 2 nên A, B, C không thỏa mãn. (4xy có biến y; 6x 3 có bậc của x là 3; x 5 có bậc của x là 5).
Vậy đa thức \({{\mathop{\rm x}\nolimits} ^5} + 4{x^3} - 6{x^2}\) chia hết cho đơn thức 4x 2 .
Ghép mỗi ý ở cột A với mỗi ý ở cột B để được kết quả đúng.
a. \(\frac{{{x^3} + 6{x^2} + 12x + 8}}{{x + 2}} = \)
b. Phân thức nghịch đảo của phân thức \(\frac{{x + y}}{{x - y}}\)
c. Phân thức đối của phân thức \(\frac{3}{{x - y}}\)
1. \(\frac{{x - y}}{{x + y}}\)
2. \(\frac{{ - 3}}{{x - y}}\)
3. x 2 + 4x + 4
a. \(\frac{{{x^3} + 6{x^2} + 12x + 8}}{{x + 2}} = \)
3. x 2 + 4x + 4
b. Phân thức nghịch đảo của phân thức \(\frac{{x + y}}{{x - y}}\)
1. \(\frac{{x - y}}{{x + y}}\)
c. Phân thức đối của phân thức \(\frac{3}{{x - y}}\)
2. \(\frac{{ - 3}}{{x - y}}\)
Sử dụng kiến thức về phân thức đại số.
a. \(\frac{{{x^3} + 6{x^2} + 12x + 8}}{{x + 2}} = \frac{{{{\left( {x + 2} \right)}^3}}}{{x + 2}} = {\left( {x + 2} \right)^2} = {x^2} + 4x + 4\) nên a – 3.
b. Phân thức nghịch đảo của phân thức \(\frac{{x + y}}{{x - y}}\) là: \(1:\frac{{x + y}}{{x - y}} = \frac{{x - y}}{{x + y}}\) nên b – 1.
c. Phân thức đối của phân thức \(\frac{3}{{x - y}}\) là: \( - \left( {\frac{3}{{x - y}}} \right) = \frac{{ - 3}}{{x - y}}\) nên c – 2.
Đáp án: a – 3 ; b – 1 ; c – 2 .
Hình thang cân là hình thang
-
A.
có hai cạnh bên bằng nhau.
-
B.
có hai cạnh đáy bằng nhau.
-
C.
có hai góc kề một cạnh bên bù nhau.
-
D.
có hai góc kề một đáy bằng nhau.
Đáp án : D
Sử dụng khái niệm hình thang cân.
Hình thang cân là hình thang có hai góc kề một đáy bằng nhau.
Cho tam giác ABC, qua điểm D thuộc cạnh BC, kẻ các đường thẳng song song với AB và AC, cắt AC và AB theo thứ tự ở E và F. Tam giác ABC cần thêm điều kiện gì thì AEDF là chữ nhật?
-
A.
cân tại A.
-
B.
vuông tại A.
-
C.
vuông cân tại A.
-
D.
\(\widehat A = {60^0}\).
Đáp án : B
Sử dụng dấu hiệu nhận biết hình vuông.

Vì DE // AF; DF // AE (gt) => AEDF là hình bình hành.
Để hình bình hành AEDF là hình chữ nhật thì \(\widehat A = {90^0}\) hay tam giác ABC vuông tại A.
Cho tam giác ABC vuông tại A có AB = \(\frac{1}{2}\)BC, đường trung tuyến AM. Tam giác ABM là tam giác gì?
-
A.
vuông tại A.
-
B.
cân tại M.
-
C.
đều.
-
D.
cân tại B.
Đáp án : C
Dựa vào kiến thức về đường trung tuyến ứng với cạnh huyền trong tam giác vuông.

Ta có tam giác ABC vuông tại A, AM là đường trung tuyến nên AM = \(\frac{1}{2}\)BC = BM = MC.
Mà AB = \(\frac{1}{2}\)BC (gt)
=> AM = AB = BM hay tam giác ABM đều.
Cho hình chóp tam giác đều có độ dài cạnh bên bằng 4 cm và độ dài cạnh đáy bằng 3cm như hình bên dưới, hình nào là hình khai triển của hình chóp tam giác đều đã cho?

-
A.
Hình a).
-
B.
Hình b).
-
C.
Hình c).
-
D.
Không có hình nào.
Đáp án : B
Sử dụng kiến thức về hình chóp tam giác đều.
Hình khai triển của chóp tam giác đều có độ dài cạnh bên bằng 4 cm và độ dài cạnh đáy bằng 3cm là hình b.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 3cm, chiều cao của hình chóp là h = 2cm. Thể tích của hình chóp đã cho là :
-
A.
6 cm \(^3\).
-
B.
18 cm \(^3\).
-
C.
12 cm \(^3\).
-
D.
9 cm \(^3\).
Đáp án : A
Dựa vào công thức tính thể tích hình chóp tứ giác.
Thể tích hình chóp S.ABCD là: \(V = \frac{1}{3}{S_d}.h = \frac{1}{3}{3^2}.2 = 6\left( {c{m^3}} \right)\).
Hai đường chéo hình thoi có độ dài 8cm và 10cm. Cạnh của hình thoi có độ dài là:
-
A.
\(6cm\).
-
B.
\(\sqrt {41} cm\).
-
C.
\(\sqrt {164} cm\).
-
D.
\(9cm\).
Đáp án : B
Sử dụng định lí Pythagore để tính.
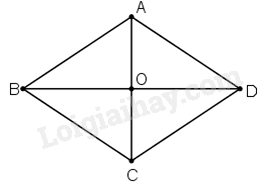
Xét hình thoi ABCD có AC = 8cm; BD = 10cm nên AO = 4 cm và OD = 5cm.
Áp dụng định lí Pythagore vào tam giác vuông OAD, ta có:
\(AD = \sqrt {O{A^2} + O{D^2}} = \sqrt {{4^2} + {5^2}} = \sqrt {41} \left( {cm} \right)\)
Một số con vật sống trên cạn: Cá voi, chó, mèo , bò. Trong các dữ liệu trên, dữ liệu chưa hợp lí là:
-
A.
Cá voi.
-
B.
Chó.
-
C.
Mèo.
-
D.
Bò.
Đáp án : A
Xác định xem con vật nào không sống trên cạn.
Dữ liệu chưa hợp lí là cá voi, vì cá voi không sống trên cạn.
Trong cuộc khảo sát tìm hiểu về cách học của học sinh khối 8 được kết quả như sau:

Có 50 % học sinh học qua đọc, viết.
Có 35 % học sinh học qua nghe
Có 10 % học sinh học qua vận động.
Có 5 % học sinh học qua quan sát.
Khẳng định nào sau đây là đúng?
-
A.
Kết quả thu thập trên là dữ liệu không phải là số.
-
B.
Kết quả thu thập trên là số liệu.
-
C.
Kết quả trên gồm cả dữ liệu không phải là số và số liệu.
-
D.
Kết quả trên dữ liệu phần trăm là dữ liệu không phải là số.
Đáp án : C
Dựa vào phân loại dữ liệu.
Các hình thức học: đọc viết; nghe; vận động; quan sát không phải là số.
Số lượng học sinh có cách học qua đọc, viết; nghe; vận động; quan sát lần lượt là: 50%, 30%, 10%, 5% là số liệu.
Vậy chọn đáp án C.
a) Kiểm tra điều kiện của mẫu thức.
b) Rút gọn biểu thức A.
c) Thay x = 10 để tính giá trị biểu thức.
d) Để biểu thức A nguyên thì mẫu thức phải là ước của tử thức.
a) Điều kiện xác định của biểu thức A là:
\(\left\{ \begin{array}{l}x + 4 \ne 0\\x - 4 \ne 0\\{x^2} - 16 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ne - 4\\x \ne 4\end{array} \right.\)
Vậy điều kiện xác định của biểu thức A là \(x \ne \pm 4\).
b) Ta có:
\(\begin{array}{l}A = \frac{1}{{x + 4}} + \frac{x}{{x - 4}} + \frac{{24 - {x^2}}}{{{x^2} - 16}}\\ = \frac{{x - 4}}{{\left( {x + 4} \right)\left( {x - 4} \right)}} + \frac{{x\left( {x + 4} \right)}}{{\left( {x + 4} \right)\left( {x - 4} \right)}} + \frac{{24 - {x^2}}}{{\left( {x + 4} \right)\left( {x - 4} \right)}}\\ = \frac{{x - 4 + {x^2} + 4x + 24 - {x^2}}}{{\left( {x + 4} \right)\left( {x - 4} \right)}}\\ = \frac{{5x + 20}}{{\left( {x + 4} \right)\left( {x - 4} \right)}}\\ = \frac{{5\left( {x + 4} \right)}}{{\left( {x + 4} \right)\left( {x - 4} \right)}}\\ = \frac{5}{{x - 4}}\end{array}\)
c) Tại x = 10 (thỏa mãn điều kiện xác định), ta được: \(A = \frac{5}{{10 - 4}} = \frac{5}{6}\).
d) Biểu thức A nguyên \( \Leftrightarrow \frac{5}{{x - 4}}\) nguyên. \(\frac{5}{{x - 4}}\) nguyên khi và chỉ khi \(\left( {x - 4} \right) \in U\left( 5 \right) = \left\{ { \pm 1; \pm 5} \right\}\).
Ta có bảng giá trị sau:
|
x – 4 |
-1 |
1 |
-5 |
5 |
|
x |
3 (TM) |
5 (TM) |
-1 (TM) |
9 (TM) |
|
\(A = \frac{5}{{x - 4}}\) |
-5 |
5 |
-1 |
1 |
Dựa vào các phép tính với đa thức, các hằng đẳng thức để rút gọn A.
a) Ta có:
\(\begin{array}{l}A = \left( {x + 5} \right)\left( {x + 1} \right) + \left( {x - 2} \right)\left( {{x^2} + 2x + 4} \right) - x\left( {{x^2} + x - 2} \right)\\ = \left( {{x^2} + 5x + x + 5} \right) + \left( {{x^3} - {2^3}} \right) - \left( {{x^3} + {x^2} - 2x} \right)\\ = {x^2} + 6x + 5 + {x^3} - 8 - {x^3} - {x^2} + 2x\\ = \left( {{x^3} - {x^3}} \right) + \left( {{x^2} - {x^2}} \right) + \left( {6x + 2x} \right) + \left( {5 - 8} \right)\\ = 8x - 3\end{array}\)
b) 74 2 + 24 2 – 48.74 = 74 2 + 24 2 – 2.24.74 = (74 – 24) 2 = 50 2 = 2 500.
Biểu đồ đoạn thẳng biểu diễn vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta qua các năm 2015; 2017; 2018; 2019; 2020. (đơn vị: nghìn tỷ đồng)

(Nguồn: Niên giám thống kê 2021)
a) Lập bảng thống kê vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta qua các năm 2015; 2017; 2018; 2019; 2020 theo mẫu sau:
|
Năm |
2015 |
2017 |
2018 |
2019 |
2020 |
|
Vốn (nghìn tỷ đồng) |
? |
? |
? |
? |
? |
b) Năm nào vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta là nhiều nhất? ít nhất?
c) Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng bao nhiêu phần trăm so năm 2015 (làm tròn kết quả đến hàng phần mười) ?
d) Năm 2017 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước giảm bao nhiêu phần trăm so năm 2019 (làm tròn kết quả đến hàng phần mười) ?
Dựa vào biểu đồ để trả lời câu hỏi.
a)
|
Năm |
2015 |
2017 |
2018 |
2019 |
2020 |
|
Vốn (nghìn tỷ đồng) |
6944,9 |
9087,3 |
9465,6 |
9357,8 |
10284,2 |
b) Vốn sản xuất kinh doanh bình quân hàng năm của doanh nghiệp nhà nước của nước ta nhiều nhất là năm 2020; ít nhất là năm 2015.
c) Tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước năm 2020 so với năm 2015 là: \(\frac{{10284,2}}{{6944,9}}.100\% = 148,1\% \)
Năm 2020 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước tăng 148,1% - 100% = 48,1% so năm 2015.
d) Tỉ số phần trăm vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước năm 2017 so với năm 2019 là \(\frac{{9087,3}}{{9357,8}}.100\% = 97,1\% \)
Năm 2017 vốn sản xuất kinh doanh bình quân của doanh nghiệp nhà nước giảm 100% - 97,1% = 2,9% so năm 2019.
1. Dựa vào định lí Pythagore để tính.
2.
a) Tứ giác AKCM là hình chữ nhật.
b) Chứng minh AKMB có hai cạnh đối song song và bằng nhau.
c) AKCM là hình vuông thì các cạnh phải bằng nhau.
1.
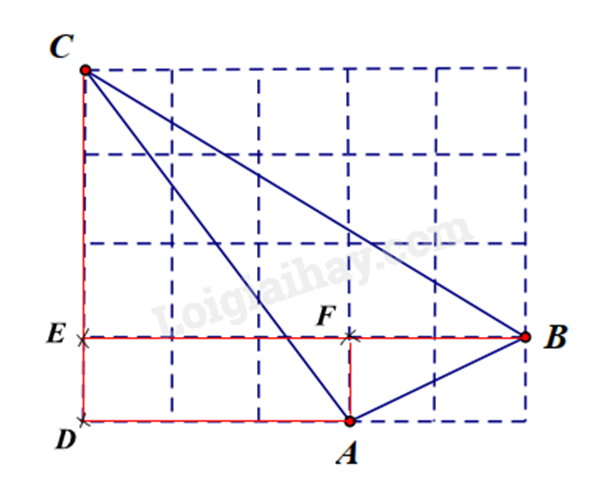
Gọi các điểm D, E và F như trên hình vẽ. Khi đó ta có các tam giác vuông ACD vuông tại D; BCE vuông tại E và ABF vuông tại F.
Tam giác ACD có AD = 3cm; CD = 4cm. Áp dụng định lí Pythagore vào tam giác ADC, ta có:
\(\begin{array}{l}A{C^2} = A{D^2} + C{D^2} = {3^2} + {4^2} = 25\\ \Rightarrow AC = 5cm\end{array}\)
Tam giác BCE có BE = 5cm; CE = 3cm. Áp dụng định lí Pythagore vào tam giác BCE, ta có:
\(\begin{array}{l}B{C^2} = B{E^2} + C{E^2} = {5^2} + {3^2} = 34\\ \Rightarrow BC = \sqrt {34} cm\end{array}\)
Tam giác ABF có AF = 1cm; BF = 2cm. Áp dụng định lí Pythagore vào tam giác ABF, ta có:
\(\begin{array}{l}A{B^2} = A{F^2} + F{B^2} = {1^2} + {2^2} = 5\\ \Rightarrow AB = \sqrt 5 cm\end{array}\)
2.
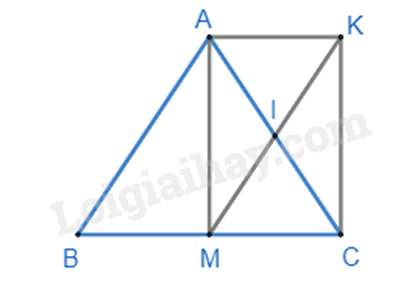
a) Xét tứ giác AKCM có: I là trung điểm của AC; I là trung điểm của KM (vì M đối xứng với K qua I)
=> AKCM là hình bình hành.
Xét tam giác ABC cân tại A có M là trung điểm của BC nên AM là đường trung tuyến đồng thời là đường cao của tam giác ABC. => \(\widehat {AMC} = {90^0}\).
Hình bình hành AKCM có \(\widehat {AMC} = {90^0}\) nên là hình chữ nhật.
b) Ta có AKCM là hình chữ nhật nên AK // CM và AK = CM.
Mà BM = CM nên BM = AK và BM // AK. => Tứ giác AKMB là hình bình hành.
c) Để AKCM là hình chữ nhật thì AM = MC = \(\frac{1}{2}\) Mà AM là đường trung tuyến của tam giác ABC nên khi đó AM là đường trung tuyến ứng với cạnh huyền của tam giác ABC hay tam giác ABC vuông tại A.
Sử dụng hằng đẳng thức để biến đổi biểu thức.
\(\begin{array}{l}A = - {x^2} + \frac{2}{3}x - 1\\ = - \left( {{x^2} - 2x.\frac{1}{3} + \frac{1}{9} - \frac{1}{9} + 1} \right)\\ = - \left[ {{x^2} - 2x.\frac{1}{3} + {{\left( {\frac{1}{3}} \right)}^2} + \frac{8}{9}} \right]\\ = - \left[ {{{\left( {x - \frac{1}{3}} \right)}^2} + \frac{8}{9}} \right] = - {\left( {x - \frac{1}{3}} \right)^2} - \frac{8}{9}\end{array}\)
Ta có \( - {\left( {x - \frac{1}{3}} \right)^2} \le 0\) nên \( - {\left( {x - \frac{1}{3}} \right)^2} - \frac{8}{9} < 0\) với mọi x.
Vậy A < 0 hay luôn luôn âm với mọi giá trị x.