Đề thi học kì 2 Toán 6 - Đề số 11 - Cánh diều — Không quảng cáo

Dựa vào kiến thức về phân số.

$\frac{{ - 2}}{5} = \frac{{ - 2.3}}{{5.3}} = \frac{{ - 6}}{{15}}$.

Đáp án C.

So sánh 2 phân số có cùng mẫu số dương, phân số nào có tử lớn hơn thì lớn hơn.

Ta có $5 < 8$ nên $- 5 >  - 8$ suy ra $\frac{{ - 5}}{7} > \frac{{ - 8}}{7}$ hay a > b.

Đáp án A.

Chuyển vế để tìm x.

$\begin{array}{l}6,72 - x = 6,3\\x = 6,72 - 6,3\\x = 0,42\end{array}$

Đáp án B.

Qua hai điểm bất kỳ chỉ có một đường thẳng đi qua chúng.

Có 1 đường thẳng đi qua hai điểm A, B cho trước.

Đáp án B.

Dựa vào kiến thức về trung điểm của đoạn thẳng.

Nếu $IA = IB = \frac{{AB}}{2}$ thì điểm $I$ là trung điểm của đoạn $AB$ nên D đúng.

Đáp án D.

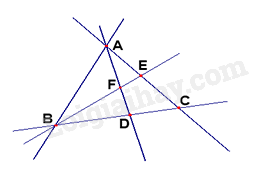
Liệt kê các bộ 3 điểm thẳng hàng.

Các bộ ba điểm thẳng hàng trong hình là: (A, E, C), (A, F, D), (B, F, E), (B, D, C).

Vậy có 4 bộ.

Đáp án C.

Số thập phân âm nhỏ hơn 0.

$- 3,16 < 0$ nên $- 3,16$ là số thập phân âm.

Đáp án B.

Dựa vào kiến thức so sánh hai số thập phân.

Ta có: $12,304 < 12,403$ nên $- 12,304 >  - 12,403$.

Đáp án A.

Xác định các đường thẳng song song.

Các cặp đường thẳng song song là: KM và QO, KQ và MO, KT và SO, KS và TO.

Đáp án B.

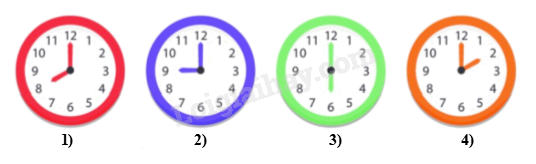
Quan sát hình vẽ để trả lời.

Trong các hình trên, hình 4 có góc tạo bởi hai kim đồng hồ là góc nhọn.

Đáp án D.

Dựa vào kiến thức về các loại góc.

Trong các khẳng định trên, chỉ có khẳng định “Góc có số đo $140^\circ$ là góc tù” là khẳng định đúng.

Đáp án D.

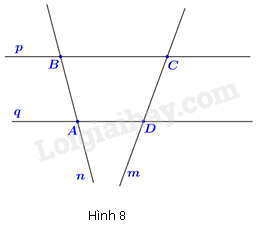
Quan sát hình vẽ để xác định.

n và q cắt nhau nên A sai.

m và n không song song nên khi kéo dài sẽ có điểm chung nên B sai.

Ba điểm A, B, C không thẳng hàng nên C đúng.

m và p cắt nhau tại C nên D sai.

Đáp án C.

Sử dụng các quy tắc tính với phân số và số thập phân.

a) $\frac{{ - 1}}{3} + \,\frac{7}{6} + \frac{3}{2} = \frac{{ - 2}}{6} + \frac{7}{6} + \frac{9}{6} = \frac{{14}}{7} = \frac{7}{3}$.

b) $\left( {\frac{1}{4} - \frac{5}{6}} \right):\frac{5}{2} = \left( {\frac{3}{{12}} - \frac{{10}}{{12}}} \right).\frac{2}{5} = \frac{7}{{12}}.\frac{2}{5} = \frac{7}{6}$.

c) $\left( { - 2,25} \right) + 7,63 = 7,63 - 2,25 = 5,38$.

d) $\left( { - 8,5} \right).16,35 - 8,5.83,65$$= \left( { - 8,5} \right).\left( {16,35 + 83,65} \right)$$= \left( { - 8,5} \right).100$$= - 850$.

e) $\frac{{{2^2}}}{{1.3}}.\frac{{{3^2}}}{{2.4}}.\frac{{{4^2}}}{{3.5}}.\frac{{{5^2}}}{{4.6}} = \frac{{2.2.3.3.4.4.5.5}}{{1.2.3.3.4.4.5.6}} = \frac{2}{6} = \frac{1}{3}$.

a) Tính số phần mà diện tích lát gạch chiếm.

Tính diện tích sân vườn thông qua diện tích phần lát gạch.

b) Tính diện tích phần trồng cỏ.

Từ đó tính được số tiền ông Ba cần để mua cỏ.

a) Diện tích phần lát gạch chiếm:

$1 - \frac{1}{5} = \frac{4}{5}$ (sân vườn)

Diện tích sân vườn:

$36\;:\frac{4}{5} = 45\;\left( {{m^2}} \right)$

b) Diện tích phần trồng cỏ:

$45 - 36 = 10\;\left( {{m^2}} \right)$

Số tiền ông Ba mua cỏ là:

$10\;.\;50\;000 = 500\;000$ (đồng)

a) Đưa các phân số về cùng mẫu dương rồi so sánh tử số với nhau.

b) Hai phân số được gọi là nghịch đảo nếu tích của chúng bằng 0.

c) Sử dụng quy tắc làm tròn số.

a) Ta có: $\frac{1}{2} = \frac{2}{4}$.

Vì $- 3 <  - 2 < 2 < 3 < 7$ nên $\frac{{ - 3}}{4} < \frac{{ - 2}}{4} < \frac{2}{4} < \frac{3}{4} < \frac{7}{4}$ hay $\frac{{ - 3}}{4} < \frac{{ - 2}}{4} < \frac{1}{2} < \frac{3}{4} < \frac{7}{4}$.

b) Các phân số nghịch đảo là: $\frac{{13}}{2};\, - 15$.

c) Số 12,057 làm tròn đến hàng phần trăm là 12,06.

Số 40,1534 làm tròn đến hàng phần trăm là 40,15.

1) a) Tính AB dựa vào OA và OB.

b) Sử dụng tính chất của trung điểm để xác định.

2) Dựa vào kiến thức về góc để kể tên.

Ta có hình vẽ sau:

a) Vì điểm A nằm giữa O và B nên OA < OB, do đó:

OA + AB = OB

hay 3 + AB = 6

AB = 6 – 3 = 3 (cm)

b) Vì OA = AB = 3cm.

Mà điểm A nằm giữa hai điểm O và B nên A là trung điểm của OB.

2) Trong hình trên có các góc: $\widehat {HOK},\widehat {KOL},\widehat {HOL}$.

Sử dụng kiến thức $\frac{{b - a}}{{a.b}} = \frac{1}{a} - \frac{1}{b}$ để tính A.

$\begin{array}{l}A = \frac{2}{{4.9}} + \frac{2}{{9.14}} + \frac{2}{{14.19}} + ... + \frac{2}{{44.49}}\\ = \frac{2}{5}\left( {\frac{5}{{4.9}} + \frac{5}{{9.14}} + \frac{5}{{14.19}} + ... + \frac{5}{{44.49}}} \right)\end{array}$

= $\frac{2}{5}.\left( {\frac{1}{4} - \frac{1}{9} + \frac{1}{9} - \frac{1}{{14}} + \frac{1}{{14}} - \frac{1}{{19}} + ... + \frac{1}{{44}} - \frac{1}{{49}}} \right)$

= $\frac{2}{5}.\left( {\frac{1}{4} - \frac{1}{{49}}} \right) = \frac{2}{5}.\frac{{45}}{{196}} = \frac{9}{{98}}$