Đề thi học kì 2 Toán 6 - Đề số 12 - Cánh diều — Không quảng cáo

Hai phân số được gọi là đối nhau nếu tổng của chúng bằng 0.

Số đối của phân số \(\frac{{ - 5}}{4}\) là \(\frac{5}{4}\).

Đáp án C.

Phân số có dạng \(\frac{a}{b}\) với \(a,b \in \mathbb{Z},b \ne 0\).

\(\frac{{ - 2}}{5}\) cho ta phân số.

Đáp án D.

Hai phân số \(\frac{a}{b} = \frac{c}{d}\left( {b,d \ne 0} \right)\) nếu \(a.d = c.b\)

\(\begin{array}{l}\frac{{ - 7}}{5} = \frac{x}{5}\\ - 7.5 = x.5\\5x =  - 35\\x =  - 7\end{array}\)

Đáp án A.

Dựa vào kiến thức về hỗn số.

Hỗn số \(5\frac{1}{3}\) có 5 là phần số nguyên và \(\frac{1}{3}\) là phần phân số nên ta chọn đáp án B.

Đáp án B.

Dựa vào kiến thức về số thập phân.

Ta có: \(\frac{{ - 2023}}{{10}} =  - 202,3\).

Đáp án D.

Dựa vào kiến thức về số thập phân.

Ta có: \(0,15 = \frac{{15}}{{100}} = \frac{{3.5}}{{20.5}} = \frac{3}{{20}}\).

Đáp án D.

Dựa vào kiến thức về điểm và đường thẳng.

Điểm A thuộc đường thẳng d thì được kí hiệu là \(A \in d\).

Đáp án A.

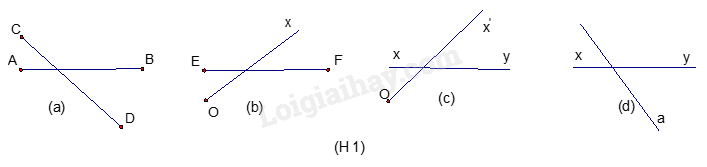
Quan sát xem hình vẽ nào biểu diễn hai đường thẳng cắt nhau.

Hình a là hình biểu diễn đoạn thẳng AB cắt đoạn thẳng CD.

Hình b là hình biểu diễn đoạn thẳng EF cắt tia Ox.

Hình c là hình biểu diễn đường thẳng xy cắt tia Ox’.

Hình d là hình biểu diễn đường thẳng xy cắt đường thẳng a nên chọn đáp án D.

Đáp án D.

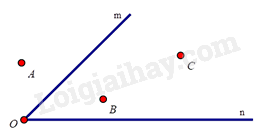
Quan sát hình vẽ để trả lời.

Các điểm B, C nằm trong góc mOn.

Đáp án C.

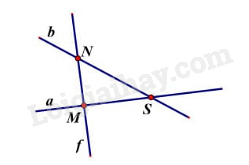
Quan sát hình vẽ để trả lời.

Hai điểm M và S thuộc đường thẳng a nên ta chọn đáp án C.

Đáp án C.

Dựa vào kiến thức về đường thẳng.

Hai đường thẳng a, b bất kì có thể song song, cắt nhau hoặc trùng nhau nên đáp án D đúng.

Đáp án D.

So sánh số đo các góc trên để chọn câu sai.

Vì \({60^0} < {90^0}\) nên \(\widehat B < \widehat D\).

Vì \({30^0} < {60^0}\) nên \(\widehat A < \widehat B\).

Vì \({110^0} > {90^0}\) nên \(\widehat C > \widehat D\) (C sai).

Vì \({60^0} < {110^0}\) nên \(\widehat B < \widehat C\).

Đáp án C.

Sử dụng quy tắc so sánh phân số và số thập phân.

a) Vì 2 < 3 nên -2 > -3

Do đó \(\frac{{ - 2}}{7} > \frac{{ - 3}}{7}\)

b) Vì 5,140 > 5,139 nên 5,14 > 5,139.

Sử dụng quy tắc tính với phân số.

\(\begin{array}{l}\frac{1}{2} - \frac{5}{4}.\frac{{ - 7}}{{10}}\\ = \frac{1}{2} - \frac{{ - 7}}{8}\\ = \frac{1}{2} + \frac{7}{8}\\ = \frac{4}{8} + \frac{7}{8}\\ = \frac{{11}}{8}\end{array}\)

a) Sử dụng thước kẻ để vẽ đoạn thẳng.

b) Sử dụng quy tắc so sánh số thập phân để so sánh AB và CD.

c) Quan sát hình vẽ để trả lời câu hỏi.

a) Vẽ đúng kích thước các đoạn thẳng có độ dài: AB = 5cm; CD = 3,5

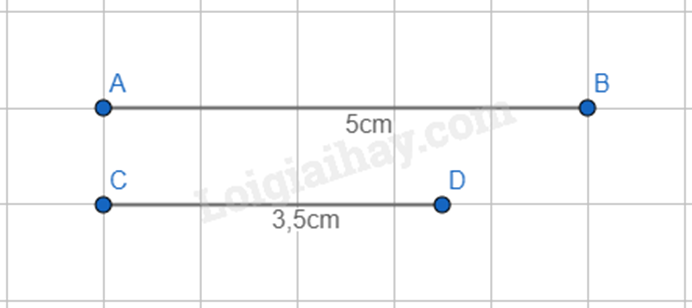
b) Vì 5 > 3,5 nên AB > CD.

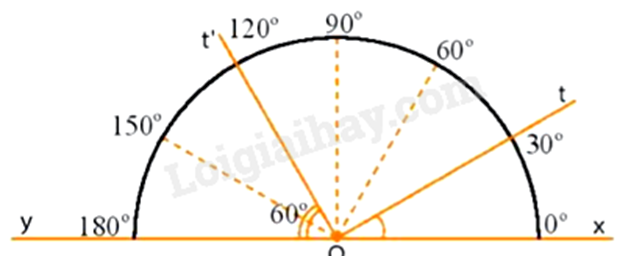
c) Số đo các góc xOt; tOt’; xOy là:

\(\begin{array}{l}\widehat {xOt} = {30^0}\\\widehat {tOt'} = \widehat {xOt'} - \widehat {xOt} = {120^0} - {30^0} = {90^0}\\\widehat {xOy} = {180^0}\end{array}\)

\(\frac{m}{n}\) của a là \(\frac{m}{n}.a\).

a) Số học sinh giỏi là: \(40.\frac{1}{5} = 8\) ( học sinh)

b) Số học sinh khá và trung bình là: 40 – 8 = 22 (học sinh)

Số học sinh trung bình là: \(22.\frac{3}{{11}} = 6\) ( học sinh)

c) Số học sinh khá là: 22 - 6 = 16 ( học sinh)

Tỉ số phần trăm số học sinh khá so với cả lớp là:

\(\frac{{16}}{{40}}.100\%  = 40\% \)

Nhóm thừa số chung để tìm x.

\(\begin{array}{l}{x^3} - {x^2} + x - 1 = 0\\{x^2}(x - 1) + (x - 1) = 0\\(x - 1)({x^2} + 1) = 0\end{array}\)

Suy ra x - 1= 0 hoặc \({x^2} + 1 = 0\)

Mà \({x^2} \ge 0\) với mọi x nên \({x^2} + 1\)> 0

Vậy x = 1