Giải bài 1. 20 trang 29 Chuyên đề học tập Toán 11 Kết nối tri thức — Không quảng cáo

Đề bài

Cho hình thang ABCD có hai đáy AB và CD, CD = 2AB. Gọi O là giao của hai cạnh bên và I là giao của hai đường chéo. Tìm ảnh của đoạn thẳng AB qua các phép vị tự V _{(O, 2)} , V _{(I, – 2)} .

Lời giải chi tiết

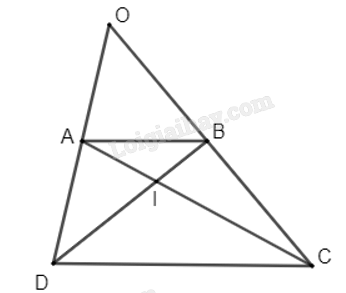
+ Vì ABCD là hình thang có hai đáy AB và CD nên AB // CD. Theo định lí Thales trong tam giác OCD ta có: $\frac{{OA}}{{OD}} = \frac{{OB}}{{OC}} = \frac{{AB}}{{CD}} = \frac{1}{2}$.

Suy ra $\overrightarrow {OD}  = 2\overrightarrow {OA} ;\,\,\overrightarrow {OC}  = 2\overrightarrow {OB}$.

Do đó, D và C tương ứng là ảnh của A và B qua phép vị tự ${V_{\left( {O,2} \right)}}$. Vậy đoạn thẳng DC là ảnh của đoạn thẳng AB qua phép vị tự ${V_{\left( {O,2} \right)}}$.

+ Vì AB // CD nên theo hệ quả của định lí Thales trong tam giác ICD ta có:

$\frac{{IA}}{{IC}} = \frac{{IB}}{{ID}} = \frac{{AB}}{{CD}} = \frac{1}{2}$

Suy ra $\overrightarrow {IC}  =  - 2\overrightarrow {IA} ;\,\,\overrightarrow {ID}  =  - 2\overrightarrow {IB}$.

Do đó, C và D tương ứng là ảnh của A và B qua phép vị tự ${V_{\left( {I,-2} \right)}}$. Vậy đoạn thẳng CD là ảnh của đoạn thẳng AB qua phép vị tự ${V_{\left( {I,-2} \right)}}$.