Giải bài 1.22 trang 29 Chuyên đề học tập Toán 11 Kết nối tri thức
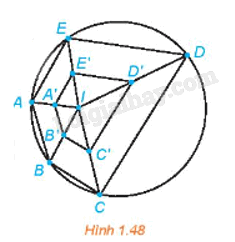
Ở Hình 1.48, A', B', C', D', E' tương ứng là trung điểm của các đoạn thẳng IA, IB, IC, ID, IE. Hỏi năm điểm đó có thuộc một đường tròn hay không? Vì sao?
Đề bài
Ở Hình 1.48, A', B', C', D', E' tương ứng là trung điểm của các đoạn thẳng IA, IB, IC, ID, IE. Hỏi năm điểm đó có thuộc một đường tròn hay không? Vì sao?
Phương pháp giải - Xem chi tiết
Quan sát hình 1.48 và dựa vào kiến thức về phép vị tự: Nếu phép vị tự tâm O tỉ số k \(\left( {k \ne 0} \right)\) lần lượt biến 2 điểm A, B thành 2 điểm A’, B’ thì \(A'B' = \left| k \right|AB\)
Lời giải chi tiết
Vì A', B', C', D', E' tương ứng là trung điểm của các đoạn thẳng IA, IB, IC, ID, IE nên ta suy ra \(\overrightarrow {IA'} = \frac{1}{2}\overrightarrow {IA} ;\,\overrightarrow {IB'} = \frac{1}{2}\overrightarrow {IB} ;\,\overrightarrow {IC'} = \frac{1}{2}\overrightarrow {IC} ;\,\overrightarrow {ID'} = \frac{1}{2}\overrightarrow {ID} ;\,\,\overrightarrow {IE'} = \frac{1}{2}\overrightarrow {IE} \). Do đó, A', B', C', D', E' tương ứng là ảnh của các điểm A, B, C, D, E qua phép vị tự tâm I, tỉ số \(\frac{1}{2}\).
Từ Hình 1.48, ta thấy các điểm A, B, C, D, E cùng thuộc một đường tròn. Vậy các điểm A', B', C', D', E' đều cùng thuộc một đường tròn là ảnh của đường tròn đi qua 5 điểm A, B, C, D, E qua phép vị tự tâm I, tỉ số \(\frac{1}{2}\).