Giải bài 1.26 trang 31 Chuyên đề học tập Toán 11 Kết nối tri thức
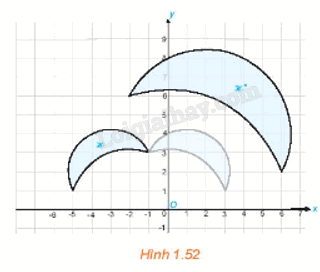
Hai hình ℋ và ℋ " trong Hình 1.52 được vẽ trên mặt phẳng tọa độ Oxy.
Đề bài
Hai hình ℋ và ℋ " trong Hình 1.52 được vẽ trên mặt phẳng tọa độ Oxy. Bằng quan sát, hãy chỉ ra một phép đối xứng trục f và một phép vị tự g sao cho phép đồng dạng có được bằng cách thực hiện liên tiếp hai phép f và g (thực hiện f trước, g sau) biến hình ℋ thành hình ℋ ".
Phương pháp giải - Xem chi tiết
Quan sát hình 1.52 để làm
Lời giải chi tiết
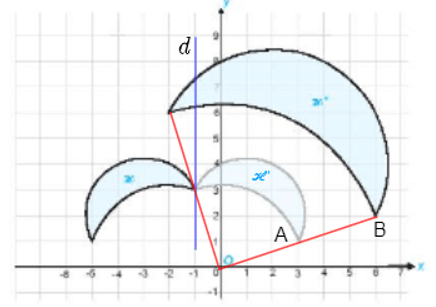
Quan sát Hình 1.52, ta thấy phép đối xứng trục d: x = – 1 biến hình ℋ thành hình ℋ '.
Ta thấy A(3; 1) thuộc hình ℋ ' và B(6; 2) thuộc hình ℋ ''.
Ta có \(\overrightarrow {OB} = \left( {6;\,2} \right)\) suy ra \(\overrightarrow {OB} = 2\overrightarrow {OA} \), khi đó phép vị tự tâm O, tỉ số 2 biến điểm A thành điểm B, thực hiện tương tự với các điểm khác, vậy ta có phép vị tự tâm O, tỉ số 2 biến hình ℋ ' thành hình ℋ ''.
Vậy phép đồng dạng có được bằng cách thực hiện liên tiếp phép đối xứng trục d có phương trình x = – 1 và phép vị tự \({V_{\left( {O,2} \right)}}\;\) (phép đối xứng trục trước, phép vị tự sau) biến hình ℋ thành hình ℋ ''.
Khi đó, phép đối xứng trục f là phép đối xứng trục d có phương trình x = – 1 và phép vị tự g là phép vị tự \({V_{\left( {O,2} \right)}}\;\)là các phép biến hình cần tìm.