Giải bài 1. 31 trang 33 Chuyên đề học tập Toán 11 Kết nối tri thức — Không quảng cáo

Đề bài

Cho đường thẳng d và hai điểm A, B cùng thuộc một nửa mặt phẳng bờ d. Hai điểm E, F thay đổi trên d sao cho $\overrightarrow {EF}$ không đổi. Xác định vị trí của hai điểm E, F để AE + BF nhỏ nhất.

Lời giải chi tiết

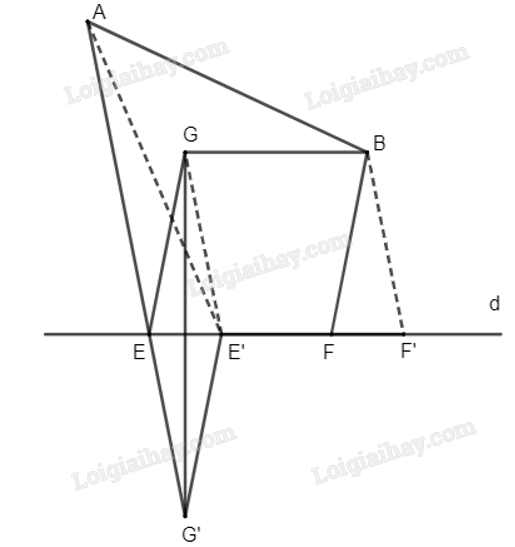
Ta có: $\left| {\overrightarrow {EF} } \right| = m\,\,(m > 0)$ không đổi.

Đặt $\vec u = \overrightarrow {EF\;} \left( {\vec u \ne \vec 0} \right),\,\vec u$ không đổi, khi đó $\mid \overrightarrow u \mid  = m$  không đổi.

Gọi G là ảnh của điểm B qua phép tịnh tiến theo vectơ $\vec u$. Khi đó $\overrightarrow {BG}  =  - \vec u$. Vì B cố định và $\overrightarrow u$ không đổi nên G cố định. Gọi G' là ảnh của G qua phép đối xứng trục d thì G' cố định.

Gọi giao điểm của AG' và đường thẳng d là E, trên d lấy điểm F thỏa mãn EF = m và $\overrightarrow {EF}  = \vec u =  - \overrightarrow {BG}$ hay $\overrightarrow {EF}  = \overrightarrow {GB}$. Khi đó BGEF là hình bình hành nên BF = GE.

Mà G và G' đối xứng nhau qua d nên GE = G'E. Do đó BF = GE = G'E.

Ta có: AE + BF = AE + G'E = AG' (1).

Ta có E và F như trên là hai điểm cần tìm để AE + BF nhỏ nhất.

Thật vậy, gọi E' và F' là 2 điểm trên d, khác E và F sao cho $\overrightarrow {E'F'}  = \vec u$  và $\left| {\overrightarrow {E'F'} } \right| = \left| {\vec u} \right| = m$.

Ta có: AE' + BF' = AE' + GE' = AE' + G'E' > AG' (2) (bất đẳng thức trong tam giác AG'E').

Từ (1) và (2) suy ra AE + BF < AE' + BF'. Từ đó suy ra điều phải chứng minh.