Giải bài 1 trang 70 SGK Toán 8 tập 2– Chân trời sáng tạo — Không quảng cáo

Đề bài

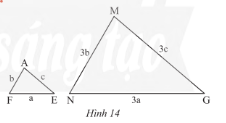
a) Tam giác $AFE$ và $MNG$ ở Hình 14 có đồng dạng với nhau không? Vì sao?

b) Biết tam giác $AFE$ có chu vi bằng 15 cm. Tính chu vi tam giác MNG.

Lời giải chi tiết

a) Ta có:

$\frac{{AF}}{{MN}} = \frac{b}{{3b}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{c}{{3c}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{a}{{3a}} = \frac{1}{3}$

Xét tam giác $AFE$ và tam giác $MNG$ có:

$\frac{{AF}}{{MN}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{1}{3} \Rightarrow \frac{{AF}}{{MN}} = \frac{{AE}}{{MG}} = \frac{{EF}}{{NG}}$

Do đó, $\Delta AFE\backsim\Delta MNG$ (c.c.c)

b) Tỉ số đồng dạng của tam giác $AFE$ và tam giác $MNG$  là $\frac{1}{3}$.

Do đó, tỉ số chu vi của của tam giác $AFE$ và tam giác $MNG$  là $\frac{1}{3}$ (tính chất)

Do đó, chu vi tam giác $MNG$ là: $15.3 = 45cm$

Vậy chu vi tam giác $MNG$ là 45 cm.