Giải bài 10 trang 58 sách bài tập toán 9 - Cánh diều tập 2
a) Vẽ đồ thị các hàm số (y = - frac{3}{2}{x^2})và (y = frac{3}{2}{x^2})trên cùng một mặt phẳng toạ độ Oxy. b) Qua đồ thị của các hàm số đó, hãy cho biết khi x tăng từ 0,5 đến 2 thì giá trị lớn nhất của hàm số (y = - frac{3}{2}{x^2}) và giá trị nhỏ nhất của hàm số (y = frac{3}{2}{x^2}) là bao nhiêu?
Đề bài
a) Vẽ đồ thị các hàm số \(y = - \frac{3}{2}{x^2}\) và \(y = \frac{3}{2}{x^2}\) trên cùng một mặt phẳng toạ độ Oxy.
b) Qua đồ thị của các hàm số đó, hãy cho biết khi x tăng từ 0,5 đến 2 thì giá trị lớn nhất của hàm số \(y = - \frac{3}{2}{x^2}\) và giá trị nhỏ nhất của hàm số \(y = \frac{3}{2}{x^2}\) là bao nhiêu?
Phương pháp giải - Xem chi tiết
- Để vẽ đồ thị hàm số bậc hai ta cần lập bảng giá trị của hàm số đó, cần ít nhất 5 giá trị để để vẽ đồ thị hàm số chuẩn hơn.
- Khi x tăng đồ thị hàm số đi lên tức là giá trị y tăng và ngược lại, do đó ta có thể dự đoán giá trị lớn nhất và giá trị nhỏ nhất
Lời giải chi tiết
a) Lập bảng giá trị của hàm số \(y = - \frac{3}{2}{x^2}\) ta được

Đồ thị hàm số \(y = - \frac{3}{2}{x^2}\) đi qua các điểm \(\left( {1; - \frac{3}{2}} \right);\) \(\left( { - 1; - \frac{3}{2}} \right);\) \(\left( {0;0} \right);\) \(\left( {2; - 6} \right);\) \(\left( { - 2; - 6} \right)\)
Lập bảng giá trị của hàm số \(y=\frac{3}{2}{{x}^{2}}\) ta được

Đồ thị hàm số \(y = \frac{3}{2}{x^2}\) đi qua các điểm \(\left( {1;\frac{3}{2}} \right);\) \(\left( { - 1;\frac{3}{2}} \right);\) \(\left( {0;0} \right);\) \(\left( {2;6} \right);\) \(\left( { - 2;6} \right)\)
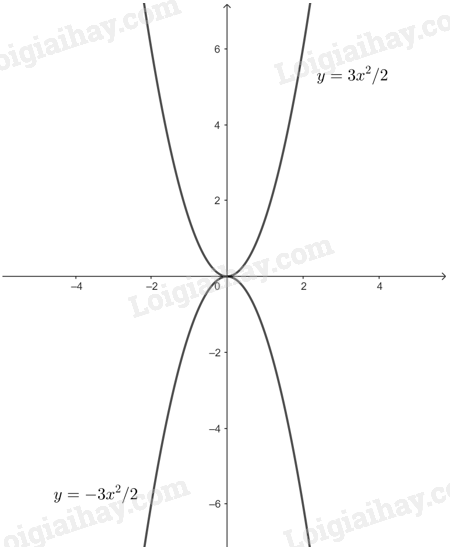
b) Qua đồ thị hàm số ta thấy khi x tăng từ 0,5 đến 2 thì giá trị lớn nhất của hàm số \(y = - \frac{3}{2}{x^2}\) lớn nhất tại \(x = 0,5\), khi đó \(y = - \frac{3}{2}.{\left( {0,5} \right)^2} = - \frac{3}{8}\).
Và khi x tăng từ 0,5 đến 2 thì giá trị nhỏ nhất của hàm số \(y = \frac{3}{2}{x^2}\) lớn nhất tại \(x = 0,5\), khi đó \(y = \frac{3}{2}.{\left( {0,5} \right)^2} = \frac{3}{8}\).