Giải bài 10 trang 84 sách bài tập toán 9 - Cánh diều tập 1 — Không quảng cáo

Đề bài

Cho tam giác ABC vuông tại C có \(AC = \frac{5}{{13}}AB\) . Tính sinA và tanB.

Lời giải chi tiết

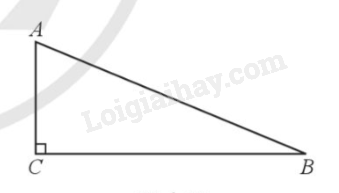
Áp dụng định lý Pythagore trong tam giác vuông ACB, ta có:

\(CB = \sqrt {A{B^2} - A{C^2}}  = \sqrt {A{B^2} - {{\left( {\frac{5}{{13}}AB} \right)}^2}}  = \frac{{12}}{{13}}AB.\)

Mặt khác \(\sin A = \frac{{CB}}{{AB}} = \left( {\frac{{12}}{{13}}AB} \right):AB = \frac{{12}}{{13}}\); \(\tan B = \frac{{AC}}{{BC}} = \left( {\frac{5}{{13}}AB} \right):\left( {\frac{{12}}{{13}}AB} \right) = \frac{5}{{12}}.\)

Vậy \(\sin A = \frac{{12}}{{13}};\tan B = \frac{5}{{12}}\).