Giải bài 11 trang 76 sách bài tập toán 11 - Chân trời sáng tạo tập 1
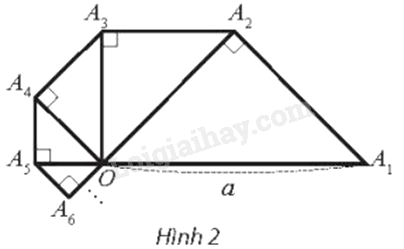
Tam giác \(O{A_1}{A_2}\) vuông cân tại \({A_2}\) có cạnh huyền \(O{A_1}\) bằng a. Bên ngoài tam giác \(O{A_1}{A_2}\), vẽ tam giác \(O{A_2}{A_3}\) vuông cân tại \({A_3}\). Tiếp theo, bên ngoài tam giác \(O{A_2}{A_3}\), vẽ tam giác \(O{A_3}{A_4}\) vuông cân tại \({A_4}\). Cứ tiếp tục quá trình như trên, ta vẽ được một dãy các hình tam giác vuông cân (Hình 2). Tính độ dài đường gấp khúc \({A_1}{A_2}{A_3}{A_4}...\)
Đề bài
Tam giác \(O{A_1}{A_2}\) vuông cân tại \({A_2}\) có cạnh huyền \(O{A_1}\) bằng a. Bên ngoài tam giác \(O{A_1}{A_2}\), vẽ tam giác \(O{A_2}{A_3}\) vuông cân tại \({A_3}\). Tiếp theo, bên ngoài tam giác \(O{A_2}{A_3}\), vẽ tam giác \(O{A_3}{A_4}\) vuông cân tại \({A_4}\). Cứ tiếp tục quá trình như trên, ta vẽ được một dãy các hình tam giác vuông cân (Hình 2). Tính độ dài đường gấp khúc \({A_1}{A_2}{A_3}{A_4}...\)
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về tổng của cấp số nhân lùi vô hạn để tính độ dài đường gấp khúc: Cấp số nhân vô hạn \(\left( {{u_n}} \right)\) có công bội q thỏa mãn \(\left| q \right| < 1\) được gọi là cấp số nhân lùi vô hạn. Cấp số nhân lùi vô hạn này có tổng là: \(S = {u_1} + {u_2} + ... + {u_n} + ... = \frac{{{u_1}}}{{1 - q}}\)
Lời giải chi tiết
Ta có các góc \(\widehat {{A_1}O{A_2}},\widehat {{A_2}O{A_3}},\widehat {{A_3}O{A_4}},...\) đều bằng \({45^0}\).
Lại có: \({A_1}{A_2} = O{A_2} = O{A_1}.\cos {45^0} = a\frac{{\sqrt 2 }}{2}\);
\({A_2}{A_3} = O{A_3} = O{A_2}.\cos {45^0} = a\frac{{\sqrt 2 }}{2}.\frac{{\sqrt 2 }}{2} = a{\left( {\frac{{\sqrt 2 }}{2}} \right)^2}\);
\({A_3}{A_4} = O{A_4} = O{A_3}.\cos {45^0} = a{\left( {\frac{{\sqrt 2 }}{2}} \right)^2}.\frac{{\sqrt 2 }}{2} = a{\left( {\frac{{\sqrt 2 }}{2}} \right)^3}\);…
Vậy độ dài các đoạn thẳng \({A_1}{A_2},{A_2}{A_3},{A_3}{A_4}...\) tạo thành cấp số nhân lùi vô hạn với số hạng đầu bằng \(a\frac{{\sqrt 2 }}{2}\) và công bội bằng \(\frac{{\sqrt 2 }}{2}\). Do đó, độ dài đường gấp khúc \({A_1}{A_2}{A_3}{A_4}...\) là: \(l = \frac{{a\sqrt 2 }}{2}.\frac{1}{{1 - \frac{{\sqrt 2 }}{2}}} = \frac{{a\sqrt 2 }}{{2 - \sqrt 2 }} = \frac{{a\sqrt 2 }}{2}\left( {2 + \sqrt 2 } \right) = a\left( {1 + \sqrt 2 } \right)\)