Giải bài 11 trang 91 sách bài tập toán 11 - Chân trời sáng tạo tập 1
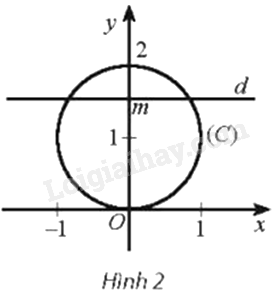
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{x^2} + {\left( {y - 1} \right)^2} = 1\). Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng \(d:y = m\) với đường tròn (C). Viết công thức xác định hàm số \(y = Q\left( m \right)\). Hàm số này không liên tục tại các điểm nào?
Đề bài
Trong mặt phẳng tọa độ Oxy, cho đường tròn \(\left( C \right):{x^2} + {\left( {y - 1} \right)^2} = 1\). Với mỗi số thực m, gọi Q(m) là số giao điểm của đường thẳng \(d:y = m\) với đường tròn (C). Viết công thức xác định hàm số \(y = Q\left( m \right)\). Hàm số này không liên tục tại các điểm nào?
Phương pháp giải - Xem chi tiết
Sử dụng kiến thức về định nghĩa hàm số liên tục tại một điểm để xét tính liên tục của hàm số: Cho hàm số \(y = f\left( x \right)\) xác định trên khoảng K và \({x_0} \in K\). Hàm số \(y = f\left( x \right)\) được gọi là liên tục tại điểm \({x_0}\) nếu \(\mathop {\lim }\limits_{x \to {x_0}} f\left( x \right) = f\left( {{x_0}} \right)\).
Lời giải chi tiết
\(Q\left( m \right) = \left\{ \begin{array}{l}0\;khi\;m < 0\;hay\;m > 2\\1\;khi\;m = 0\;hay\;m = 2\\2\;khi\;0 < m < 2\end{array} \right.\)
Vì \(\mathop {\lim }\limits_{m \to {0^ + }} Q\left( m \right) \ne \mathop {\lim }\limits_{m \to {0^ - }} Q\left( m \right)\) nên hàm số trên không liên tục tại điểm \(m = 0\).
Vì \(\mathop {\lim }\limits_{m \to {2^ + }} Q\left( m \right) \ne \mathop {\lim }\limits_{m \to {2^ - }} Q\left( m \right)\) nên hàm số trên không liên tục tại điểm \(m = 2\).
Vậy hàm số Q(m) không liên tục tại các điểm \(m = 0\), \(m = 2\).