Giải bài 12 trang 15 SBT toán 10 - Chân trời sáng tạo — Không quảng cáo

Đề bài

Thiết kế của một chiếc cổng có hình parabol với chiều cao 5 m và khoảng cách giữa hai chân cổng là 4 m.

a) Chọn trục hoành là đường thẳng nối hai chân cổng, gốc tọa độ tại một chân cổng, chân cổng còn lại có hoành độ dương, đơn vị là 1 m. Hãy viết phương trình của vòm cổng.

b) Người ta cần chuyền một thùng hàng hình hộp chữ nhật với chiều cao 3 m. Chiều rộng của thùng hàng tối đa là bao nhiêu để thùng có thể chuyển lọt qua được cổng?

Lưu ý: Đáp số làm tròn đến hàng phần trăm

Lời giải chi tiết

a) Giả sử phương trình mô tả cổng có dạng $y = a{x^2} + bx + c$

Từ cách đặt hệ trục ta có:

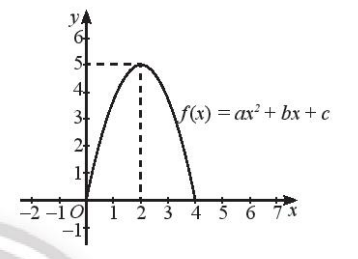
+) Gốc tọa độ tại chân cổng nên $0 = a{.0^2} + b.0 + c \Leftrightarrow c = 0$

+) Chân cổng còn lại có hoành độ bằng khoảng cách 2 chân cổng là 4 m nên $0 = a{.4^2} + b.4 + c \Leftrightarrow 16a + 4b + c = 0$

+) Đỉnh cổng có tọa độ (2;5) nên $5 = a{.2^2} + b.2 + c \Leftrightarrow 4a + 2b + c = 5$

Giải hệ phương trình lập được từ ba phương trình trên ta được $a =  - \frac{5}{4};b = 5;c = 0$

Vậy phương trình vòm cổng là $y =  - \frac{5}{4}{x^2} + 5x$

b) Yêu cầu bài toán tương đương với tìm các giá trị của x để $y \ge 3$

$\Leftrightarrow  - \frac{5}{4}{x^2} + 5x \ge 3 \Leftrightarrow  - \frac{5}{4}{x^2} + 5x - 3 \ge 0 \Leftrightarrow \frac{{10 - 2\sqrt {10} }}{5}x \le \frac{{10 + 2\sqrt {10} }}{5}$

Suy ra chiều rộng tối đa mà thùng hàng có thể qua cổng là $\frac{{10 + 2\sqrt {10} }}{5} - \frac{{10 - 2\sqrt {10} }}{5} = \frac{{4\sqrt {10} }}{5} \approx 2,53$

Vậy chiều rộng tối ra của thùng hàng gần bằng 2,53 m