Giải bài 12 trang 85 sách bài tập toán 9 - Cánh diều tập 1
Cho tam giác ABC có AB = 6cm, \(\widehat A = 15^\circ ,\widehat B = 35^\circ \). Tính độ dài đường cao CH của tam giác ABC (làm tròn kết quả đến hàng phần trăm của centimet).
Đề bài
Cho tam giác ABC có AB = 6cm, \(\widehat A = 15^\circ ,\widehat B = 35^\circ \). Tính độ dài đường cao CH của tam giác ABC (làm tròn kết quả đến hàng phần trăm của centimet).
Phương pháp giải - Xem chi tiết
Bước 1: Biểu diễn AH qua tanA và BH qua tanB.
Bước 2: Thay AH, BH vào \(AB = AH + BH\), ta tìm được CH.
Lời giải chi tiết
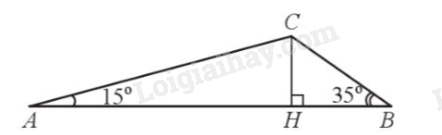
Do CH là đường cao của tam giác ABC nên \(\widehat {CHB} = \widehat {CHA} = 90^\circ \).
Xét tam giác vuông CHA ta có \(\tan A = \frac{{CH}}{{AH}}\), do đó \(AH = \frac{{CH}}{{\tan A}}\).
Xét tam giác vuông CHB ta có \(\tan B = \frac{{CH}}{{BH}}\), do đó \(BH = \frac{{CH}}{{\tan B}}\).
Mặt khác \(AB = AH + BH\), suy ra \(\frac{{CH}}{{\tan A}} + \frac{{CH}}{{\tan B}} = 6\) hay \(\frac{{CH}}{{\tan 15^\circ }} + \frac{{CH}}{{\tan 35^\circ }} = 6\)
Nên \(CH.\left( {\frac{1}{{\tan 15^\circ }} + \frac{1}{{\tan 35^\circ }}} \right) = 6\) suy ra \(CH = \frac{6}{{\left( {\frac{1}{{\tan 15^\circ }} + \frac{1}{{\tan 35^\circ }}} \right)}} \approx 1,16\left( {cm} \right)\)
Vậy \(CH \approx 1,16\)cm.