Giải bài 13 trang 111 sách bài tập toán 9 - Cánh diều tập 2
Trên mặt phẳng toạ độ Oxy cho M(–4; 0), N(4; 0) và P(3; 3). a) Phép quay ngược chiều α° tâm O biến điểm M thành điểm N. Tìm α. b) Qua phép quay thuận chiều 90° tâm O, điểm P biến thành điểm nào?
Đề bài
Trên mặt phẳng toạ độ Oxy cho M(–4; 0), N(4; 0) và P(3; 3).
a) Phép quay ngược chiều α° tâm O biến điểm M thành điểm N. Tìm α.
b) Qua phép quay thuận chiều 90° tâm O, điểm P biến thành điểm nào?
Phương pháp giải - Xem chi tiết
Dựa vào phép quay thuận chiều \({\alpha ^o}\) ( \({0^o} < {\alpha ^o} < {360^o}\) ) tâm O giữ nguyên điểm O, biến điểm M (khác điểm O) thành điểm M’ thuộc đường tròn (O; OM) sao cho tia OM quay thuận chiều kim đồng hồ đến tia OM’ thì điểm M tạo nên cung MnM’ có số đo \({\alpha ^o}\) .
Dựa vào phép quay thuận chiều \({\alpha ^o}\) ( \({0^o} < {\alpha ^o} < {360^o}\) ) tâm O được phát biểu tương tự như trên.
Lời giải chi tiết
a)
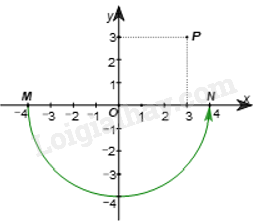
Ta có: M(–4; 0), N(4; 0) suy ra OM = |–4| = 4; ON = |4| = 4.
Do đó OM = OM. (1)
Ta cũng suy ra được điểm M và điểm N cùng nằm trên trục Ox, đối xứng với nhau qua điểm O, khi đó \(\widehat {MON} = {180^o}\) .
Do đó, tia OM quay đến tia ON theo chiều ngược kim đồng hồ tạo thành một cung có số đo bằng 180°. (2)
Từ (1) và (2), ta có phép quay ngược chiều 180° tâm O biến điểm M thành điểm N.
Vậy α = 180.
b)
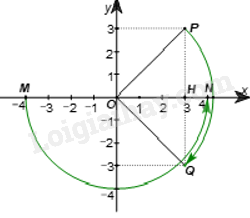
Gọi H là hình chiếu của điểm P trên Ox.
Do P(3; 3) nên H(3; 0). Suy ra OH = 3 và PH = 3.
Do đó ∆OPH vuông cân tại H, nên \(\widehat {POH} = {45^o}\) .
Gọi Q là điểm đối xứng với P(3; 3) qua Ox. Khi đó Q(3; –3).
Ta cũng chứng minh được \(\widehat {QOH} = {45^o}\) .
Khi đó, \(\widehat {POQ} = \widehat {POH} + \widehat {HOQ} = {45^o} + {45^o} = {90^o}\) .
Mặt khác, P và Q đối xứng với nhau qua Ox hay OH là trung trực của PQ, nên OP = OQ. Do đó tia OP quay đến tia OQ theo chiều kim đồng hồ tạo thành một cung có số đo bằng 90°.
Vậy phép quay thuận chiều 90° tâm O điểm P(3; 3) biến thành điểm Q(3; – 3).