Giải bài 13 trang 12 sách bài tập toán 12 - Chân trời sáng tạo
Người ta thấy rằng trong vòng 3 năm tính từ đầu năm 2020, giá thành (P) của một loại sản phẩm vào tháng thứ (t) thay đổi theo công thức (Pleft( t right) = 80{t^3} - 3600{t^2} + 48000t + 100000) (đồng) với (0 le t le 36). Hãy cho biết trong khoảng thời gian nào giá thành sản phẩm tăng, trong khoảng thời gian nào giá thành sản phẩm giảm. Giá thành đạt cực đại và cực tiểu vào thời điểm nào?
Đề bài
Người ta thấy rằng trong vòng 3 năm tính từ đầu năm 2020, giá thành \(P\) của một loại sản phẩm vào tháng thứ \(t\) thay đổi theo công thức \(P\left( t \right) = 80{t^3} - 3600{t^2} + 48000t + 100000\) (đồng) với \(0 \le t \le 36\).
Hãy cho biết trong khoảng thời gian nào giá thành sản phẩm tăng, trong khoảng thời gian nào giá thành sản phẩm giảm. Giá thành đạt cực đại và cực tiểu vào thời điểm nào?
Phương pháp giải - Xem chi tiết
Xét hàm số \(P\left( t \right)\) trên đoạn \(\left[ {0;36} \right]\), lập bảng biến thiên và tìm cực trị của hàm số.
Lời giải chi tiết
Xét hàm số \(P\left( t \right) = 80{t^3} - 3600{t^2} + 48000t + 100000\) trên đoạn \(\left[ {0;36} \right]\).
Ta có: \(P'\left( t \right) = 240{t^2} - 7200t + 48000;P'\left( t \right) = 0 \Leftrightarrow t = 10\) hoặc \(t = 20\).
Bảng biến thiên:
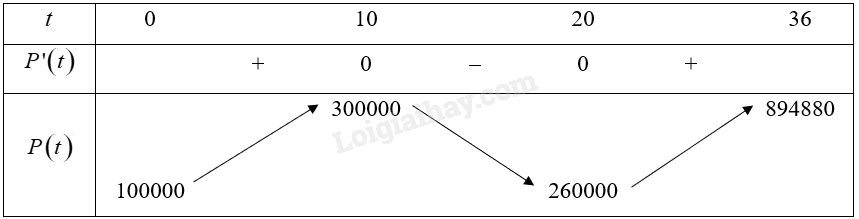
Vậy hàm số đạt cực đại tại \(x = 10\); hàm số đạt cực tiểu tại \(x = 20\).
Vậy giá thành đạt cực đại tại thời điểm 10 tháng và giá thành đạt cực tiểu vào thời điểm 20 tháng.