Giải bài 13 trang 77 sách bài tập toán 11 - Chân trời sáng tạo tập 1
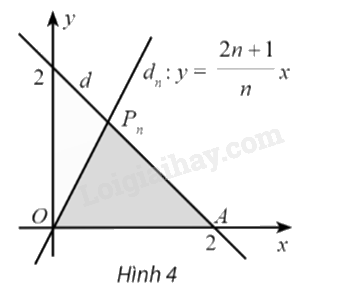
Trong mặt phẳng tọa độ Oxy, đường thẳng \(d:x + y = 2\) cắt trục hoành tại điểm A và cắt đường thẳng \({d_n}:y = \frac{{2n + 1}}{n}x\) tại điểm \({P_n}\left( {n \in \mathbb{N}*} \right)\). Kí hiệu \({S_n}\) là diện tích của tam giác \(OA{P_n}\). Tính \(\lim {S_n}\).
Đề bài
Trong mặt phẳng tọa độ Oxy, đường thẳng \(d:x + y = 2\) cắt trục hoành tại điểm A và cắt đường thẳng \({d_n}:y = \frac{{2n + 1}}{n}x\) tại điểm \({P_n}\left( {n \in \mathbb{N}*} \right)\). Kí hiệu \({S_n}\) là diện tích của tam giác \(OA{P_n}\). Tính \(\lim {S_n}\).
Phương pháp giải - Xem chi tiết
+ Sử dụng kiến thức về các phép toán về giới hạn hữu hạn của dãy số để tính: Cho \(\lim {u_n} = a,\lim {v_n} = b\) và c là hằng số: \(\lim \left( {{u_n} + {v_n}} \right) = a + b\), \(\lim \left( {c.{u_n}} \right) = c.a\), \(\lim \frac{{{u_n}}}{{{v_n}}} = \frac{a}{b}\left( {b \ne 0} \right)\).
+ Sử dụng kiến thức về một số giới hạn cơ bản để tính: \(\lim {q^n} = 0\) (q là số thực, \(\left| q \right| < 1\)), \(\lim c = c\) (c là hằng số).
Lời giải chi tiết
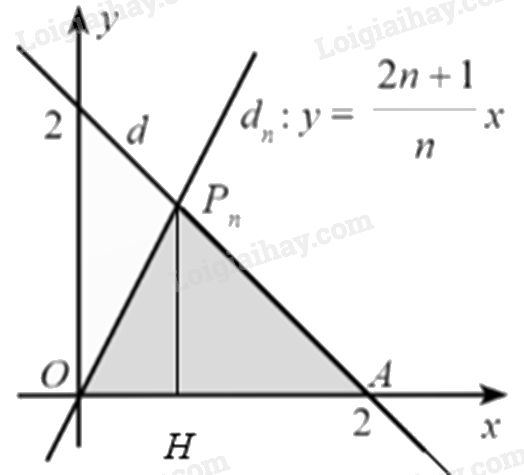
Ta có: \(A\left( {0;2} \right);OA = 2;\widehat {OA{P_n}} = {45^0}\)
Vì P là giao điểm của \({d_n}\) và d nên tọa độ của P là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}x + y = 2\\y = \frac{{2n + 1}}{n}x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x + \frac{{2n + 1}}{n}x = 2\\y = \frac{{2n + 1}}{n}x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x.\frac{{3n + 1}}{n} = 2\\y = \frac{{2n + 1}}{n}x\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = \frac{{2n}}{{3n + 1}}\\y = \frac{{4n + 2}}{{3n + 1}}\end{array} \right.\)
Do đó, \({P_n}\left( {\frac{{2n}}{{3n + 1}};\frac{{4n + 2}}{{3n + 1}}} \right)\)
Gọi H là hình chiếu vuông góc của \({P_n}\) trên trục Ox.
Khi đó: \({P_n}H = \left| {\frac{{4n + 2}}{{3n + 1}}} \right| = \frac{{4n + 2}}{{3n + 1}}\left( {do\;n \in \mathbb{N}*} \right)\)
Diện tích tam giác \(OA{P_n}\) là: \({S_n} = \frac{1}{2}.OA.{P_n}H = \frac{1}{2}.2.\frac{{4n + 2}}{{3n + 1}} = \frac{{4n + 2}}{{3n + 1}}\)
\(\lim {S_n} = \lim \frac{{4n + 2}}{{3n + 1}} = \lim \frac{{4 + \frac{2}{n}}}{{3 + \frac{1}{n}}} = \frac{4}{3}\)