Giải bài 14 trang 106 sách bài tập toán 9 - Cánh diều tập 1 — Không quảng cáo

Đề bài

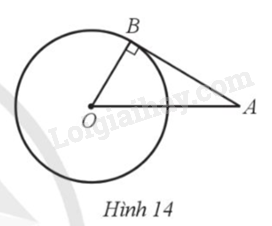
Cho đường tròn (O;R) và điểm A sao cho OA = 2R. Kẻ tiếp tuyến AB của đường tròn (O; R) với B là tiếp điểm (hình 14). Tính độ dài đoạn thẳng AB theo R.

Lời giải chi tiết

Do tiếp tuyến AB của đường tròn (O; R) nên OB vuông góc với AB.

Áp dụng định lý Pythagore trong tam giác vuông OBA ta có

$AB = \sqrt {O{A^2} - O{B^2}}  = \sqrt {{{\left( {2R} \right)}^2} - {R^2}}  = R\sqrt 3$.

Vậy $AB = R\sqrt 3$.