Giải Bài 15 trang 70 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC có AB < AC, AD là tia phân giác của \(\widehat {BAD}\) (D ∈ BC). Chứng minh \(\widehat {ADB} < \widehat {ADC}\) .
Đề bài
Cho tam giác ABC có AB < AC, AD là tia phân giác của \(\widehat {BAD}\) (D ∈ BC). Chứng minh \(\widehat {ADB} < \widehat {ADC}\) .
Phương pháp giải - Xem chi tiết
Áp dụng quan hệ giữa góc và cạnh đối diện và tổng ba góc trong một tam giác để chứng minh \(\widehat {ADB} < \widehat {ADC}\)
Lời giải chi tiết
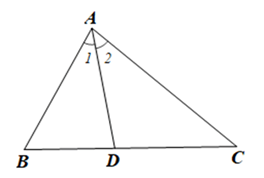
Xét tam giác ABC có AB < AC (giả thiết)
Suy ra \(\hat C < \hat B\) (trong một tam giác, góc đối diện với cạnh lớn hơn là góc lớn hơn).
Vì AD là tia phân giác của góc BAC nên \({\widehat {{A^{}}}_1} = {\widehat {{A^{}}}_2}\)
Xét ∆ABD có: \({\widehat {{A^{}}}_1} + \widehat B + \widehat {ADB} = 180^\circ \) (tổng ba góc của một tam giác).
Suy ra \(\widehat {A{\rm{D}}B} = 180^\circ - \widehat {{A_1}^{}} - \widehat B\) (1)
Xét ∆ACD có: \(\widehat {{A_2}^{}} + \widehat C + \widehat {A{\rm{D}}C} = 180^\circ \) (tổng ba góc của một tam giác).
Suy ra \(\widehat {A{\rm{D}}C} = {180^o} - \widehat {{A_2}^{}} - \widehat C\) (2)
Mà \(\widehat {{A_1}} = \widehat {{A_2}}\) (chứng minh trên) và \(\widehat B > \widehat C\) (chứng minh trên) (3)
Từ (1), (2) và (3) ta có \(\widehat {A{\rm{D}}B} < \widehat {A{\rm{D}}C}\)
Vậy \(\widehat {A{\rm{D}}B} < \widehat {A{\rm{D}}C}\)