Giải bài 18 trang 66 sách bài tập toán 8 – Cánh diều
Cho hình chữ nhật \(ABCD\). Kẻ \(CH\) vuông góc với \(BD\left( {H \in BD} \right)\). Gọi \(I,K,M\) lần lượt là trung điểm của \(BH,CH,AD\). Chứng minh:
Đề bài
Cho hình chữ nhật \(ABCD\). Kẻ \(CH\) vuông góc với \(BD\left( {H \in BD} \right)\). Gọi \(I,K,M\) lần lượt là trung điểm của \(BH,CH,AD\). Chứng minh:
a) Tứ giác \(IKDM\) là hình bình hành;
b) Gọi \(N\) là giao điểm của \(IM\) và \(AH\). Hỏi \(IN\) có thể là đường trung bình của tam giác \(HAB\) không? Vì sao?
Phương pháp giải - Xem chi tiết
Định nghĩa: Đường trung bình của tam giác là đoạn thẳng nối trung điểm hai cạnh tam giác đó.
Tính chất: Đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh đó.
Lời giải chi tiết
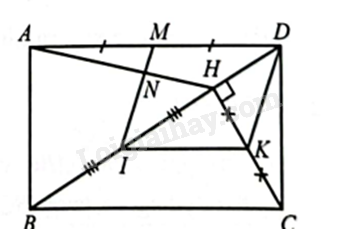
a) \(I,K\) lần lượt là trung điểm của \(BH,CH\) nên \(IK = \frac{{BC}}{2},IK//BC\). Vì \(IK//BC\) và \(MD//BC\) nên \(IK//MD\) (1). Vì \(IK = \frac{{BC}}{2},MD = \frac{{BC}}{2}\) nên \(IK = MD\) (2).
Từ (1) và (2) suy ra tứ giác \(IKDM\) là hình bình hành.
b) Nếu \(IN\) là đường trung bình của tam giác \(HAB\) thì \(IN//AB\). Suy ra \(IM//AB\). Mà \(MA = MD\), suy ra \(I\) là trung điểm của \(BD\) (3). Mặt khác theo giả thiết, \(I\) là trung điểm của \(HB\) (4). Từ (3) và (4) suy ra vô lí. Vậy \(IN\) không thể là đường trung bình của tam giác \(HAB\).