Giải bài 19 trang 95 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Cho hình tứ diện ABCD có \(AB \bot \left( {BCD} \right),\)các tam giác BCD và ACD là những tam giác nhọn. Gọi H, K lần lượt là trực tâm của các tam giác BCD, ACD. Chứng minh rằng:

a) \(AD \bot CH;\)

b*) \(HK \bot \left( {ACD} \right).\)

Lời giải chi tiết

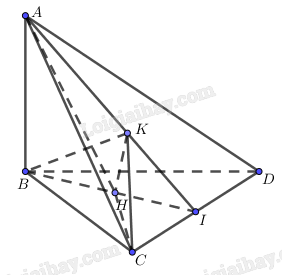
a) Vì \(AB \bot \left( {BCD} \right),{\rm{ }}CH \subset \left( {BCD} \right) \Rightarrow AB \bot CH.\) Do H là trực tâm của tam giác (BCD) nên \(CH \bot BD.\)

Mà AB, BD cắt nhau trong mặt phẳng (ABD) nên \(CH \bot \left( {ABD} \right).\)

Từ \(CH \bot \left( {ABD} \right),{\rm{ }}AD \subset \left( {ABD} \right) \Rightarrow AD \bot CH.\)

b*) Vì H là trực tâm của tam giác BCD nên \(BH \bot CD.\)

Lại có, \(AB \bot \left( {BCD} \right),{\rm{ }}CD \subset \left( {BCD} \right) \Rightarrow AB \bot CD.\)

Mà AB, BD cắt nhau trong mặt phẳng (ABI) nên \(CD \bot \left( {ABI} \right).\)

Từ \(CD \bot \left( {ABI} \right),{\rm{ }}HK \subset \left( {ABI} \right) \Rightarrow CD \bot HK.\)

Vì K là trực tâm của tam giác ACD nên \(CK \bot AD.\) Mà CK, CH cắt nhau trong mặt phẳng (CHK) nên \(AD \bot \left( {CHK} \right).\)

Lại có, \(AD \bot \left( {CHK} \right),{\rm{ }}HK \subset \left( {CHK} \right) \Rightarrow AD \bot HK.\)

Bên cạnh đó, AD, CD cắt nhau trong mặt phẳng (ACD) nên \(HK \bot \left( {ACD} \right).\)