Giải bài 2. 35 trang 47 SGK Toán 8 tập 1 - Kết nối tri thức — Không quảng cáo

Đề bài

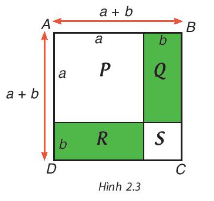
Sử dụng Hình 2.3, bằng cách tính diện tích hình vuông ABCD theo hai cách, hãy giải thích hằng đẳng thức \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\).

Lời giải chi tiết

Diện tích hình vuông ABCD là: \({\left( {a + b} \right)^2}\)

Diện tích hình vuông ABCD là:

\({S_{ABCD}} = {S_P} + {S_Q} + {S_R} + {S_S} \)

\(= {a^2} + ab + ab + {b^2} \)

\(= {a^2} + 2ab + {b^2}\)

Do đó \({\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}\)