Giải bài 2 trang 107 SGK Toán 7 tập 2 - Cánh diều — Không quảng cáo

Đề bài

Cho tam giác ABC cân tại A , hai đường trung tuyến BM và CN cắt nhau tại G. Chứng minh:

a) BM = CN; b) $\Delta GBC$ cân tại G .

Lời giải chi tiết

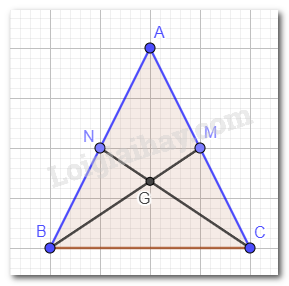
a) Tam giác ABC cân tại A nên AB = AC. M, N lần lượt là trung điểm của cạnh AC, AB nên AM = AN .

Xét tam giác ABM và tam giác ACN có: AM = AN ; $\widehat A$chung; AB = AC .

Vậy $\Delta ABM = \Delta ACN$(c.g.c) hay BM = CN .

b) Xét tam giác ABC có G là giao điểm của hai đường trung tuyến BM và CN nên G là trọng tâm tam giác ABC . Do đó:

$GB = \dfrac{2}{3}BM;GC = \dfrac{2}{3}CN$. Mà BM = CN nên GB = GC .

Vậy tam giác GBC cân tại G .