Giải bài 2 trang 79 sách bài tập toán 9 - Chân trời sáng tạo tập 2
Cho tam giác ABC có đường cao AH (H( in )BC) và nội tiếp đường tròn (O). Vẽ đường kính AD của đường tròn (O). Chứng minh AB.AC = AH.AD
Đề bài
Cho tam giác ABC có đường cao AH (H \( \in \) BC) và nội tiếp đường tròn (O). Vẽ đường kính AD của đường tròn (O). Chứng minh AB.AC = AH.AD
Phương pháp giải - Xem chi tiết
Chứng minh \(\Delta \)AHB và \(\Delta \)ACD đồng dạng với nhau rồi suy ra tỉ số đồng dạng.
Lời giải chi tiết
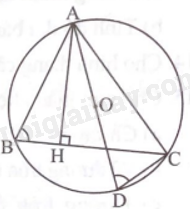
Ta có \(\widehat {ACD}\) là góc nội tiếp chắn nửa đường tròn (O) nên \(\widehat {ACD} = {90^o}\).
Xét \(\Delta \)AHB và \(\Delta \)ACD có \(\widehat {AHB} = \widehat {ACD} = {90^o}\)
\(\widehat {ABH} = \widehat {ADC}\) (hai góc nội tiếp cùng chắn cung AC).
Do đó \(\Delta \)AHB \(\backsim \) \(\Delta \)ACD (g.g).
Suy ra \(\frac{{AB}}{{AD}} = \frac{{AH}}{{AC}}\) hay AB.AC = AH. AD.
Cùng chủ đề:
Giải bài 2 trang 79 sách bài tập toán 9 - Chân trời sáng tạo tập 2