Giải bài 2 trang 92 sách bài tập toán 9 - Chân trời sáng tạo tập 1
Cho đường tròn (O; R) và dây cung MN = (Rsqrt 3 ). Tính số đo của mỗi cung (oversetfrown{MN}) (cung lớn và cung nhỏ).
Đề bài
Cho đường tròn (O; R) và dây cung MN = \(R\sqrt 3 \) . Tính số đo của mỗi cung \(\overset\frown{MN}\) (cung lớn và cung nhỏ).
Phương pháp giải - Xem chi tiết
Dựa vào: Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó. Số đo của cung lớn bằng hiệu giữa 360 o và số đo cung nhỏ có chung hai đầu mút với cung lớn.
Lời giải chi tiết
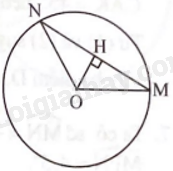
Kẻ \(OH \bot MN\) tại H. Ta có OM = ON = R, suy ra tam giác OMN cân tại O, suy ra HM = HN.
Dó đó HM = HN = \(\frac{{MN}}{2} = \frac{{R\sqrt 3 }}{2}\) .
Ta có: \(cos\widehat {HMO} = \frac{{HM}}{2} = \frac{{\frac{{R\sqrt 3 }}{2}}}{R} = \frac{{\sqrt 3 }}{2},\)
Nên \(\widehat {HMO} = {30^o}\) , suy ra \(\widehat {MON} = {120^o}\) .
Suy ra số đo cung nhỏ \(\overset\frown{MN}\) là 120 o , số đo cung lớn \(\overset\frown{MN}\) = 360 o – 120 o = 240 o .