Giải bài 2 trang 96 SGK Toán 7 tập 2 - Cánh diều — Không quảng cáo

Đề bài

Cho tam giác ABC có $\widehat A = 120^\circ$. Tia phân giác của góc A cắt cạnh BC tại D . Đường thẳng qua D song song với AB cắt cạnh AC tại E . Chứng minh rằng tam giác ADE đều.

Lời giải chi tiết

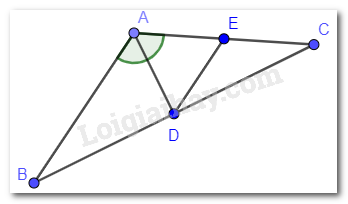
Vì $\widehat A = 120^\circ$ nên $\widehat {DAE} = 60^\circ$ ( AD là phân giác của góc A ).

Ta có: DE // AB nên $\widehat {CED} = \widehat {EAB} = 120^\circ$ (hai góc đồng vị).

Ba điểm A, E, C thẳng hàng nên góc AEC bằng 180°

Suy ra $\widehat {AED} = 180^\circ  - \widehat {CED} = 180^\circ  - 120^\circ  = 60^\circ$

Tam giác ADE có $\widehat {EAD} = \widehat {ADE}$ ($=60^0$) nên là tam giác cân.

Mà $\widehat {DEA} = 60^\circ$

Do đó, tam giác ADE đều ( tam giác cân có 1 góc bằng $60^0$).