Giải bài 20 trang 80 SBT toán 10 - Cánh diều — Không quảng cáo

Đề bài

Quan sát cây cầu dây văng minh họa ở Hình 25

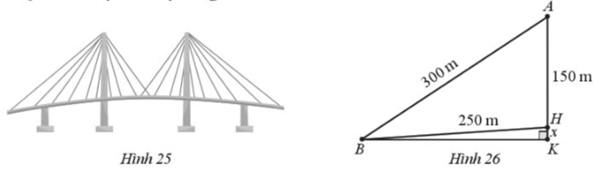
Tại trụ cao nhất, khoảng cách từ đỉnh trụ (vị trí A ) tới chân trụ trên mặt cầu (vị trí H ) là 150 m, độ dài dây văng dài nhất nối từ đỉnh trụ xuống mặt cầu (vị trí B ) là 300 m, khoảng cách từ chân dây văng dài nhất tới chân trụ trên mặt cầu là 250 m (Hình 26). Tính độ dốc của cầu qua trụ nói trên (làm tròn kết quả đến hàng phần mười theo đơn vị độ).

Lời giải chi tiết

Áp dụng định lí cosin cho ∆ ABH ta có: $A{B^2} = B{H^2} + A{H^2} - 2.BH.AH.\cos \widehat {AHB}$

$\Rightarrow \cos \widehat {AHB} = \frac{{B{H^2} + A{H^2} - A{B^2}}}{{2.BH.AH}} = \frac{{{{250}^2} + {{150}^2} - {{300}^2}}}{{2.250.150}} =  - \frac{1}{{15}}$$\Rightarrow \widehat {AHB} \approx 93,{8^0}$

Xét ∆ HBK có $\widehat {AHB}$ là góc ngoài của tam giác HBK

$\Rightarrow \widehat {AHB} = \widehat {HBK} + \widehat {HKB} \Rightarrow \widehat {HBK} = \widehat {AHB} - \widehat {HKB} = 93,{8^0} - {90^0} = 3,{8^0}$

Vậy độ dốc của cầu qua trụ là 3,8 ⁰