Giải bài 22 trang 91 sách bài tập toán 9 - Cánh diều tập 2
Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O;R). E là điểm tùy ý trên cung nhỏ AC. Gọi I là giao điểm của EB và AC. Kẻ IK vuông góc với AB. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì EK luôn đi qua một điểm cố định.
Đề bài
Cho tam giác ABC vuông cân tại C và nội tiếp đường tròn (O;R). E là điểm tùy ý trên cung nhỏ AC. Gọi I là giao điểm của EB và AC. Kẻ IK vuông góc với AB. Chứng minh rằng khi E di chuyển trên cung nhỏ AC thì EK luôn đi qua một điểm cố định.
Phương pháp giải - Xem chi tiết
Chứng minh \(\widehat {BEK} = \widehat {BED} = {45^o}\) suy ra E, K, D thẳng hàng nên khi E di chuyển trên cung nhỏ AC thì EK luôn đi qua một điểm cố định.
Lời giải chi tiết
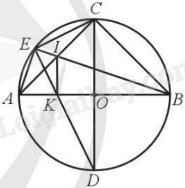
Kẻ đường kính CD suy ra D cố định.
Ta có \(\widehat {AEI} = \widehat {AKI} = {90^o}\) nên tứ giác EIKA nội tiếp đường tròn đường kính AI.
Từ đó suy ra \(\widehat {KAI} = \widehat {KEI}\).
Lại có \(\widehat {KAI} = {45^o}\) (do tam giác ACB vuông cân tại C) do đó \(\widehat {KEI} = {45^o}\) hay \(\widehat {BEK} = {45^o}\) (1).
Mặt khác, \(\widehat {BED} = {45^o}\) (do D là điểm chính giữa của cung AB) (2).
Từ (1) và (2) suy ra E, K, D thẳng hàng.
Vậy khi E di chuyển trên cung nhỏ AC thì EK luôn đi qua điểm D cố định.