Giải bài 23 trang 104 sách bài tập toán 11 - Cánh diều
Cho tứ diện\(ABCD\). Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là trung điểm của \(AB\), \(AD\), \(BC\), \(CD\).
Đề bài
Cho tứ diện\(ABCD\). Gọi \(M\), \(N\), \(P\), \(Q\) lần lượt là trung điểm của \(AB\), \(AD\), \(BC\), \(CD\). Chứng minh rằng giao tuyến của hai mặt phẳng \(\left( {APQ} \right)\) và \(\left( {CMN} \right)\) song song với đường thẳng \(BD\).
Phương pháp giải - Xem chi tiết
Sử dụng kết quả sau: Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó.
Lời giải chi tiết
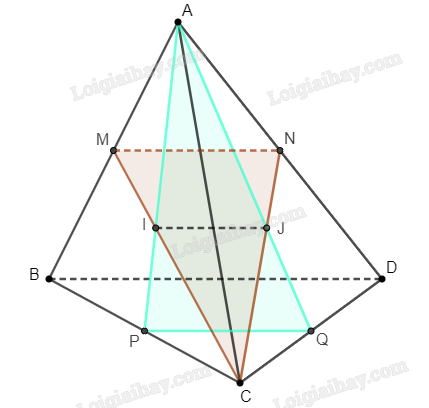
Gọi \(\left\{ I \right\} = MC \cap AP\), \(\left\{ J \right\} = NC \cap AQ\).
Do \(MC \subset \left( {CMN} \right)\), \(AP \subset \left( {APQ} \right)\) nên suy ra \(I \in \left( {APQ} \right) \cap \left( {CMN} \right)\).
Tương tự ta cũng có \(J \in \left( {APQ} \right) \cap \left( {CMN} \right)\). Như vậy \(IJ\) là giao tuyến của hai mặt phẳng \(\left( {APQ} \right)\) và \(\left( {CMN} \right)\).
Ta có \(M\) là trung điểm của \(AB\), \(N\) là trung điểm của \(AD\), suy ra \(MN\) là đường trung bình của tam giác \(ABD\). Từ đó ta có \(MN\parallel BD\).
Do \(MN \subset \left( {CMN} \right)\), ta suy ra \(BD\parallel \left( {CMN} \right)\).
Chứng minh tương tự, ta cũng có \(BD\parallel \left( {APQ} \right)\).
Ta có \(BD\parallel \left( {CMN} \right)\), \(BD\parallel \left( {APQ} \right)\), \(IJ\) là giao tuyến của hai mặt phẳng \(\left( {APQ} \right)\) và \(\left( {CMN} \right)\). Vậy \(BD\parallel IJ\).
Bài toán được chứng minh.