Giải bài 23 trang 95 sách bài tập toán 11 - Cánh diều
Cho đoạn thẳng AB và mặt phẳng (P) sao cho \(\left( P \right) \bot AB\) và (P)
Đề bài
Cho đoạn thẳng AB và mặt phẳng (P) sao cho \(\left( P \right) \bot AB\) và (P) cắt đoạn thẳng AB tại điểm H thoả mãn HA = 4 cm, HB = 9 cm. Điểm C chuyển động trong mặt phẳng (P) thoả mãn \(\widehat {ACB} = {90^0}.\) Chứng minh rằng điểm C thuộc đường tròn tâm H bán kính 6 cm trong mặt phẳng (P).
Phương pháp giải - Xem chi tiết
Sử dụng hệ thức lượng trong tam giác vuông để tính độ dài HC.
Lời giải chi tiết
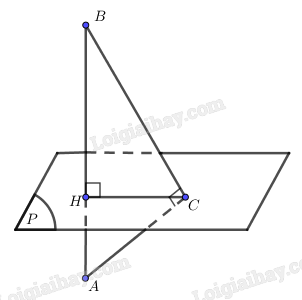
Vì \(AC \bot CB\) nên A, B, C không thẳng hàng.
Ta có: \(\left( P \right) \bot AB,{\rm{ }}HC \subset \left( P \right)\) nên \(AB \bot HC.\)
Xét \(\Delta ABC\) vuông tại C, đường cao CH. Áp dụng hệ thức lượng trong tam giác vuông ta có: \(H{C^2} = HA.HB = 4.9 = 36 \Rightarrow HC = 6\left( {{\rm{cm}}} \right).\)
Vậy C thuộc đường tròn tâm H bán kính 6 cm trong (P).