Giải bài 3.26 trang 57 SGK Toán 7 tập 1 - Kết nối tri thức
Cho góc xOy không phải là góc bẹt. Khẳng định nào sau đây là đúng?
Đề bài
Cho góc xOy không phải là góc bẹt. Khẳng định nào sau đây là đúng?
(1) Nếu Ot là tia phân giác của góc xOy thì \(\widehat {xOt} = \widehat {tOy}\).
(2) Nếu tia Ot thỏa mãn \(\widehat {xOt} = \widehat {tOy}\) thì Ot là tia phân giác của góc xOy.
Nếu có khẳng định không đúng, hãy nêu ví dụ cho thấy khẳng định đó không đúng.
(Gợi ý: Xét tia đối của một tia phân giác)
Phương pháp giải - Xem chi tiết
Khi Om là tia phân giác của góc xOy thì \(\widehat {xOm} = \widehat {mOy} = \frac{1}{2}.\widehat {xOy}\)
Lời giải chi tiết
(1) đúng vì Ot là tia phân giác của góc xOy thì \(\widehat {xOt} = \widehat {tOy} = \frac{1}{2}.\widehat {xOy}\)
(2) sai vì
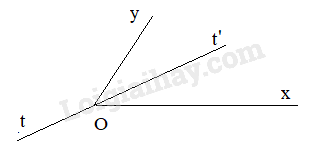
Gọi Ot’ là tia phân giác của góc xOy, ta có: \(\widehat {xOt'} = \widehat {t'Oy}\)
Xét tia Ot là tia đối của tia Ot' thì \(\widehat {xOt'}+ \widehat {xOt}= 180^0; \widehat {t'Oy}+\widehat {tOy}=180^0\) (kề bù)
Ta có: \(\widehat {xOt} = \widehat {tOy}\) nhưng Ot không là tia phân giác của góc xOy.
Chú ý:
Mỗi góc khác góc bẹt chỉ có một tia phân giác.