Giải bài 3.28 trang 66 SGK Toán 8 tập 1 - Kết nối tri thức
Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A.
Đề bài
Xét một điểm M trên cạnh huyền của tam giác ABC vuông cân tại A. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC.
a) Hỏi tứ giác MPAN là hình gì?
b) Hỏi M ở vị trí nào thì đoạn thẳng NP có độ dài ngắn nhất? Vì sao?
Phương pháp giải - Xem chi tiết
a) Xét tứ giác APMN có 3 góc vuông nên là hình chữ nhật.
b) Sử dụng tính chất của hình chữ nhật.
Lời giải chi tiết
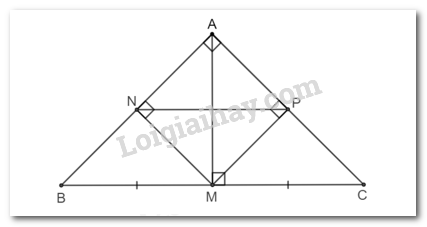
a) Tứ giác MPAN có: \(\widehat {NAP} = \widehat {APM} = \widehat {MNA} = {90^o}\)
Do đó tứ giác MPAN là hình chữ nhật.
b) Vì tứ giác MPAN là hình chữ nhật có hai đường chéo AM và NP nên AM = NP.
Để đoạn thẳng NP có độ dài ngắn nhất thì AM có độ dài ngắn nhất.
Khi đó, MA là đường vuông góc kẻ từ A đến đoạn thẳng BC hay AM là đường cao của tam giác ABC.
Mà tam giác ABC vuông cân tại A nên AM cũng là đường trung tuyến.
Do đó M là trung điểm của BC.
Vậy M là trung điểm của đoạn thẳng BC thì đoạn thẳng NP có độ dài ngắn nhất.