Giải bài 3.32 trang 72 SGK Toán 8 tập 1 - Kết nối tri thức
Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật.
Đề bài
Chứng minh rằng các trung điểm của bốn cạnh trong một hình thoi là các đỉnh của một hình chữ nhật.
Phương pháp giải - Xem chi tiết
Giả sử ABCD là hình thoi. Gọi E, H, G, F lần lượt là trung điểm của các cạnh AB; AD; DC; CB.
Chứng minh các cặp cạnh song song và bằng nhau suy ra EFGH là hình chữ nhật.
Lời giải chi tiết
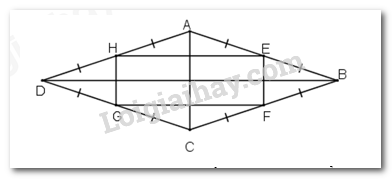
Ta cần chứng minh EFGH là hình chữ nhật. Thật vậy:
Do ABCD là hình thoi nên AB = BC = CD = DA.
Do E, H lần lượt là trung điểm của AB, AD nên AH = DH = AE = BE.
Tam giác AHE có AH = AE nên là tam giác cân tại A, suy ra \(\widehat {AHE} = \widehat {AEH}\)
Mà \(\widehat {HAE} + \widehat {AHE} + \widehat {AEH} = 180^\circ \)
Suy ra \(\widehat {AHE} = \frac{{180^\circ - \widehat {HAE}}}{2}\)
Tương tự, ta có tam giác DHG cân tại D nên \(\widehat {DHG} = \frac{{180^\circ - \widehat {HDG}}}{2}\)
Mặt khác, do ABCD là hình thoi nên AB // CD, suy ra \(\widehat {HAE} + \widehat {HDG} = 180^\circ \)
Khi đó \(\widehat {AHE} + \widehat {DHG} = \frac{{180^\circ - \widehat {HAE}}}{2} + \frac{{180^\circ - \widehat {HDG}}}{2}\)
= \(\frac{{180^\circ - \widehat {HAE} + 180^\circ - \widehat {HDG}}}{2}\)
= \(\frac{{360^\circ - (\widehat {HAE} + \widehat {HDG})}}{2}\)
= \(\frac{{360^\circ - 180^\circ }}{2}\)
Mà \(\widehat {AHE} + \widehat {DHG} + \widehat {EHG} = 180^\circ \)
Suy ra \(\widehat {EHG} = 180^\circ - (\widehat {AHE} + \widehat {DHG}) = 180^\circ - 90^\circ = 90^\circ \)
Chứng minh tương tự như trên ta cũng có \(\widehat {HEF} = \widehat {EFG} = \widehat {FGH} = {90^0}.\)
Tứ giác EFGH có bốn góc vuông nên là hình chữ nhật.