Giải bài 3. 29 trang 44 sách bài tập toán 8 - Kết nối tri thức với cuộc sống — Không quảng cáo

Đề bài

Gọi H là giao của ba đường cao AI, BJ, CK của tam giác nhọn ABC. Dùng công thức tính diện tích tam giác để chứng minh: $\frac{{HI}}{{AI}} + \frac{{HJ}}{{BJ}} + \frac{{HK}}{{CK}} = 1$

Hỏi khi góc A của tam giác ABC là góc tù thì công thức đó thay đổi thế nào?

Lời giải chi tiết

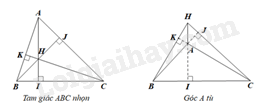
+ Trường hợp tam giác ABC nhọn:

Diện tích tam giác ABC là: ${S_{ABC}} = \frac{1}{2}IA.BC$

Diện tích tam giác HBC là: ${S_{HBC}} = \frac{1}{2}HI.BC$

Do đó, $\frac{{{S_{HBC}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}HI.BC}}{{\frac{1}{2}AI.BC}} = \frac{{HI}}{{AI}}$

Diện tích tam giác ABC là: ${S_{ABC}} = \frac{1}{2}BJ.AC$

Diện tích tam giác HAC là: ${S_{HAC}} = \frac{1}{2}HJ.AC$

Do đó, $\frac{{{S_{HAC}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}HJ.AC}}{{\frac{1}{2}BJ.AC}} = \frac{{HJ}}{{BJ}}$

Diện tích tam giác ABC là: ${S_{ABC}} = \frac{1}{2}CK.AB$

Diện tích tam giác HAB là: ${S_{HAB}} = \frac{1}{2}HK.AB$

Do đó, $\frac{{{S_{HAB}}}}{{{S_{ABC}}}} = \frac{{\frac{1}{2}HK.AB}}{{\frac{1}{2}CK.AB}} = \frac{{HK}}{{CK}}$

Vậy $\frac{{HI}}{{AI}} + \frac{{HJ}}{{BJ}} + \frac{{HK}}{{CK}} = \frac{{{S_{HBC}}}}{{{S_{ABC}}}} + \frac{{{S_{HAC}}}}{{{S_{ABC}}}} + \frac{{{S_{HAB}}}}{{{S_{ABC}}}} = 1$

Trường hợp góc A tù, H nằm trong góc đối đỉnh với góc BAC, ta có: ${S_{ABC}} = {S_{HBC}} - {S_{HAB}} - {S_{HAC}}$

Do đó, $\frac{{HI}}{{AI}} - \frac{{HJ}}{{BJ}} - \frac{{HK}}{{CK}} = 1$