Giải bài 3 trang 101 sách bài tập toán 10 - Chân trời sáng tạo
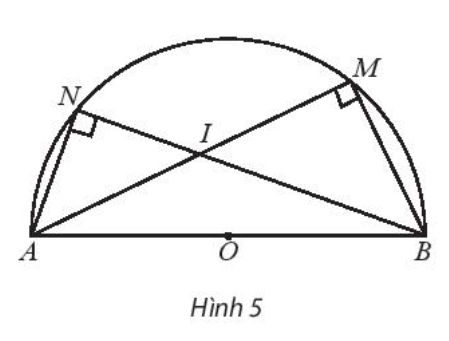
Cho nửa đường tròn tâm O có đường kính AB = 2R. Gọi M và N là hai điểm thuộc nửa đường tròn sao cho AM và BN cắt nhau tại I như hình 5.
Đề bài
Cho nửa đường tròn tâm O có đường kính \(AB = 2R\). Gọi M và N là hai điểm thuộc nửa đường tròn sao cho AM và BN cắt nhau tại I như hình 5.
a) Chứng minh: \(\overrightarrow {AI} .\overrightarrow {AM} = \overrightarrow {AI} .\overrightarrow {AB} ;\overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {AB} .\overrightarrow {BA} \)
b) Tính \(\overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN} \) theo R
Lời giải chi tiết
a) Ta có:
\(\begin{array}{l}\overrightarrow {AI} .\overrightarrow {AM} = \left| {\overrightarrow {AI} } \right|.\left| {\overrightarrow {AM} } \right|.\cos \left( {\overrightarrow {AI} ,\overrightarrow {AM} } \right)\\ = AI.AM.\cos 0^\circ = AI.AM\end{array}\) (*)
Mặt khác \(AM = AB.\cos \widehat {MAB}\), thay vào (*) ta có:
\(\begin{array}{l}\overrightarrow {AI} .\overrightarrow {AM} = AI.AM = AI.AB.\cos \widehat {MAB}\\ = \left| {\overrightarrow {AI} } \right|.\left| {\overrightarrow {AB} } \right|.\cos \left( {\overrightarrow {AI} ,\overrightarrow {AB} } \right) = \overrightarrow {AI} .\overrightarrow {AB} \end{array}\) (đpcm)
\(\begin{array}{l}\overrightarrow {BI} .\overrightarrow {BN} = \left| {\overrightarrow {BI} } \right|.\left| {\overrightarrow {BN} } \right|.\cos \left( {\overrightarrow {BI} ,\overrightarrow {BN} } \right)\\ = BI.BN.\cos 0^\circ = BI.BN\end{array}\) (**)
Mặt khác \(BN = BA.\cos \widehat {NBA}\), thay vào (**) ta có:
\(\begin{array}{l}\overrightarrow {BI} .\overrightarrow {BN} = BI.BN = BI.BA.\cos \widehat {NBA}\\ = \left| {\overrightarrow {BI} } \right|.\left| {\overrightarrow {BA} } \right|.\cos \left( {\overrightarrow {BI} ,\overrightarrow {BA} } \right) = \overrightarrow {BI} .\overrightarrow {BA} \end{array}\) (đpcm)
b) Từ kết quả của câu a) ta có:
\(\begin{array}{l}\overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN} = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\overrightarrow {BA} = \overrightarrow {AI} .\overrightarrow {AB} + \overrightarrow {BI} .\left( { - \overrightarrow {AB} } \right)\\ = \overrightarrow {AI} .\overrightarrow {AB} - \overrightarrow {AB} .\overrightarrow {BI} = \overrightarrow {AB} \left( {\overrightarrow {AI} - \overrightarrow {BI} } \right) = \overrightarrow {AB} \left( {\overrightarrow {AI} + \overrightarrow {IB} } \right) = {\overrightarrow {AB} ^2}\\ = A{B^2} = {\left( {2R} \right)^2} = 4{R^2}\end{array}\)
Vậy \(\overrightarrow {AI} .\overrightarrow {AM} + \overrightarrow {BI} .\overrightarrow {BN} = 4{R^2}\)