Giải bài 3 trang 102 SGK Toán 10 tập 1 – Chân trời sáng tạo — Không quảng cáo

Đề bài

Cho hình thoi ABCD đi có cạnh bằng a và có góc A bằng $60^\circ$. Tìm độ dài của các vectơ sau: $\overrightarrow p  = \overrightarrow {AB}  + \overrightarrow {AD} ;\overrightarrow u  = \overrightarrow {AB}  - \overrightarrow {AD} ;\overrightarrow v  = 2\overrightarrow {AB}  - \overrightarrow {AC}$.

Lời giải chi tiết

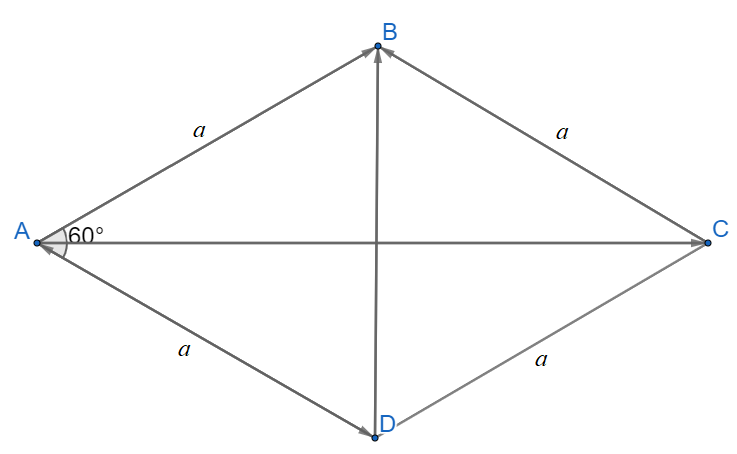
+) ABCD là hình thoi nên cũng là hình bình hành

Áp dụng quy tắc hình bình hành ta có:

$\overrightarrow p  = \overrightarrow {AB}  + \overrightarrow {AD}  = \overrightarrow {AC}$

$\Rightarrow  |\overrightarrow p|  = | \overrightarrow {AC}| =AC$

+) $\overrightarrow u  = \overrightarrow {AB}  - \overrightarrow {AD}  = \overrightarrow {DB}$

$\Rightarrow  |\overrightarrow u|  = | \overrightarrow {DB}| =DB$

+) $\overrightarrow v  = 2\overrightarrow {AB}  - \overrightarrow {AC}  = \overrightarrow {AB}  + \left( {\overrightarrow {AB}  - \overrightarrow {AC} } \right) = \overrightarrow {AB}  + \overrightarrow {CB}$$= \overrightarrow {AB}  + \overrightarrow {DA}  = \overrightarrow {DB}$

$\Rightarrow  |\overrightarrow v|  = | \overrightarrow {DB}| =DB$

+ Tính $AC, DB$

Tam giác ABD có $AB=AD=a, \widehat A = 60^o$ nên nó là tam giác đều. Do đó DB = a.

Gọi O là giao điểm hai đường chéo.

Ta có: $AO = AB. \sin B = a. \sin 60^o = \frac {a \sqrt 3}{2} \Rightarrow  AC = a \sqrt 3$

Vậy $|\overrightarrow p|  =  a \sqrt 3 ,|\overrightarrow u|  =  a, |\overrightarrow v|  =  a.$