Giải bài 3 trang 109 sách bài tập toán 12 - Chân trời sáng tạo
Nhiệt độ không khí trung bình hằng năm tại hai trạm quan trắc đặt ở Quy Nhơn và Cà Mau từ năm 2006 đến năm 2022 được ghi lại như sau: a) Hãy chia dữ liệu trên thành 4 nhóm có độ dài bằng nhau với nhóm đầu tiên là \(\left[ {26,7;27,1} \right)\). b) Hãy so sánh độ phân tán nhiệt độ không khí trung bình mỗi năm tại hai khu vực trên: ‒ theo khoảng biến thiên; – theo khoảng tứ phân vị; – theo phương sai.
Đề bài
Nhiệt độ không khí trung bình hằng năm tại hai trạm quan trắc đặt ở Quy Nhơn và Cà Mau từ năm 2006 đến năm 2022 được ghi lại như sau:

a) Hãy chia dữ liệu trên thành 4 nhóm có độ dài bằng nhau với nhóm đầu tiên là \(\left[ {26,7;27,1} \right)\).
b) Hãy so sánh độ phân tán nhiệt độ không khí trung bình mỗi năm tại hai khu vực trên:
‒ theo khoảng biến thiên;
– theo khoảng tứ phân vị;
– theo phương sai.
Phương pháp giải - Xem chi tiết
‒ Sử dụng công thức tính khoảng biến thiên của mẫu số liệu ghép nhóm: \(R = {a_{m + 1}} - {a_1}\).
‒ Sử dụng công thức tính các tứ phân vị của mẫu số liệu ghép nhóm:
Tứ phân vị thứ \(k\) được xác định như sau: \({Q_k} = {u_m} + \frac{{\frac{{kn}}{4} - C}}{{{n_m}}}\left( {{u_{m + 1}} - {u_m}} \right)\)
trong đó:
• \(n = {n_1} + {n_2} + ... + {n_k}\) là cỡ mẫu;
• \(\left[ {{u_m};{u_{m + 1}}} \right)\) là nhóm chứa tứ phân vị thứ \(k\);
• \({n_m}\) là tần số của nhóm chứa tứ phân vị thứ \(k\);
• \(C = {n_1} + {n_2} + ... + {n_{m - 1}}\).
‒ Sử dụng công thức tính khoảng tứ phân vị của mẫu số liệu ghép nhóm: \(\Delta Q = {Q_3} - {Q_1}\).
‒ Sử dụng công thức tính phương sai của mẫu số liệu ghép nhóm:
\(\begin{array}{l}{S^2} = \frac{1}{n}\left[ {{n_1}{{\left( {{c_1} - \overline x } \right)}^2} + {n_2}{{\left( {{c_2} - \overline x } \right)}^2} + ... + {n_k}{{\left( {{c_k} - \overline x } \right)}^2}} \right]\\ & = \frac{1}{n}\left[ {{n_1}c_1^2 + {n_2}c_2^2 + ... + {n_k}c_k^2} \right] - {\overline x ^2}\end{array}\)
Lời giải chi tiết
a) Bảng tần số ghép nhóm
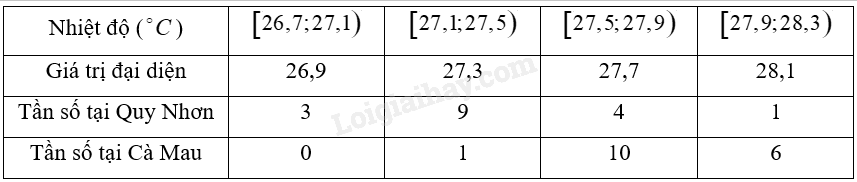
b) • Khoảng biến thiên của mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình tại Quy Nhơn là: \({R_{QN}} = 28,3 - 26,7 = 1,6\left( {^ \circ C} \right)\).
Khoảng biển thiên của mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình tại Cà Mau là: \({R_{CM}} = 28,3 - 27,1 = 1,2\left( {^ \circ C} \right)\).
Do đó, nếu so sánh theo khoảng biến thiên, nhiệt độ không khí trung bình tại Quy Nhơn phân tán hơn tại Cà Mau.
• Tứ phân vị của mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình tại Quy Nhơn:
Cỡ mẫu: \({n_{QN}} = 3 + 9 + 4 + 1 = 17\)
Gọi \({x_1};{x_2};...;{x_{17}}\) là mẫu số liệu gốc gồm nhiệt độ không khí trung bình tại Quy Nhơn theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_5} \in \left[ {27,1;27,5} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_{QN1}} = 27,1 + \frac{{\frac{{1.17}}{4} - 3}}{9}\left( {27,5 - 27,1} \right) = \frac{{1222}}{{45}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{13}} \in \left[ {27,5;27,9} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_{QN3}} = 27,5 + \frac{{\frac{{3.17}}{4} - \left( {3 + 9} \right)}}{4}\left( {27,9 - 27,5} \right) = \frac{{1103}}{{40}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\(\Delta {Q_{QN}} = {Q_{QN3}} - {Q_{QN1}} = \frac{{1103}}{{40}} - \frac{{1222}}{{45}} \approx 0,42\) (g).
Tứ phân vị của mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình tại Cà Mau:
Cỡ mẫu: \({n_{CM}} = 17\)
Gọi \({x_1};{x_2};...;{x_{17}}\) là mẫu số liệu gốc gồm nhiệt độ không khí trung bình tại Cà Mau theo thứ tự không giảm.
Tứ phân vị thứ nhất của mẫu số liệu gốc là \({x_5} \in \left[ {27,5;27,9} \right)\). Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
\({Q_{CM1}} = 27,5 + \frac{{\frac{{1.17}}{4} - 1}}{{10}}\left( {27,9 - 27,5} \right) = \frac{{2763}}{{100}}\)
Tứ phân vị thứ ba của mẫu số liệu gốc là \({x_{13}} \in \left[ {27,9;28,3} \right)\). Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
\({Q_{QN3}} = 27,9 + \frac{{\frac{{3.17}}{4} - \left( {1 + 10} \right)}}{6}\left( {28,3 - 27,9} \right) = \frac{{1681}}{{60}}\)
Khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
\(\Delta {Q_{CM}} = {Q_{CM3}} - {Q_{CM1}} = \frac{{1681}}{{60}} - \frac{{2763}}{{100}} \approx 0,39\left( {^ \circ C} \right)\).
Do đó, nếu so sánh theo khoảng tứ phân vị, nhiệt độ không khí trung bình tại Quy Nhơn phân tán hơn tại Cà Mau.
• Phương sai của mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình tại Quy Nhơn:
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline {{x_{QN}}} = \frac{{3.26,9 + 9.27,3 + 4.27,7 + 1.28,1}}{{17}} = \frac{{4653}}{{170}}\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\(S_{QN}^2 = \frac{1}{{17}}\left( {{{3.26,9}^2} + {{9.27,3}^2} + {{4.27,7}^2} + {{1.28,1}^2}} \right) - {\left( {\frac{{4653}}{{170}}} \right)^2} \approx 0,099\)
Phương sai của mẫu số liệu ghép nhóm về nhiệt độ không khí trung bình tại Cà Mau:
Số trung bình của mẫu số liệu ghép nhóm là:
\(\overline {{x_{CM}}} = \frac{{1.27,3 + 10.27,7 + 6.28,1}}{{17}} = \frac{{4729}}{{170}}\)
Phương sai của mẫu số liệu ghép nhóm đó là:
\(S_{CM}^2 = \frac{1}{{17}}\left( {{{1.27,3}^2} + {{10.27,7}^2} + {{6.28,1}^2}} \right) - {\left( {\frac{{4729}}{{170}}} \right)^2} \approx 0,052\)
Do \(S_{QN}^2 > S_{CM}^2\) nên khi so sánh theo phương sai, nhiệt độ không khí trung bình tại Quy Nhơn phân tán hơn tại Cà Mau.