Giải bài 3 trang 41 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình ℋ. Hỏi ℋ có mấy trục đối xứng?
Đề bài
Cho ba đường tròn có bán kính bằng nhau và đôi một tiếp xúc ngoài với nhau tạo thành hình ℋ. Hỏi ℋ có mấy trục đối xứng?
A. 0.
B. 1.
C. 2.
D. 3.
Phương pháp giải - Xem chi tiết
Có một đường thẳng chia hình thành hai phần bằng nhau mà nếu “gấp” hình theo đường thẳng thì hai phần đó “chồng khít” lên nhau. Được gọi là hình có trục đối xứng và đường thẳng là trục đối xứng của nó.
Lời giải chi tiết
Đáp án đúng là: D
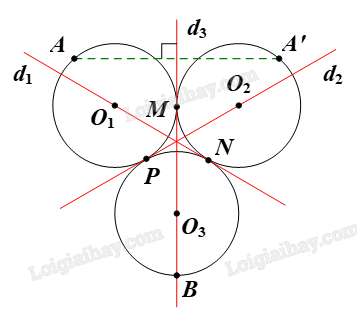
Gọi (O 1 ), (O 2 ), (O 3 ) là ba đường tròn thỏa mãn yêu cầu bài toán.
Gọi M, N, P lần lượt là tiếp điểm của các cặp đường tròn (O 1 ) và (O 2 ); (O 2 ) và (O 3 ); (O 1 ) và (O 3 ) (hình vẽ).
Chọn các đường thẳng \({Đ_1},{\rm{ }}{Đ_2},{\rm{ }}{Đ_3}\;\) lần lượt là các đường thẳng đi qua các cặp điểm O 1 và N; O 2 và P; O 3 và M.
Lấy điểm A nằm trên hình ℋ nhưng không nằm trên đường thẳng d 3 .
Ta đặt A’ là ảnh của A qua phép đối xứng trục d 3 .
Khi đó A’ nằm trên hình ℋ ban đầu.
Lấy điểm B nằm trên hình ℋ và nằm trên đường thẳng d 3 .
Ta thấy B là ảnh của chính nó qua phép đối xứng trục d 3 .
Tương tự như vậy, ta chọn các điểm khác bất kì nằm trên hình ℋ, ta cũng xác định được ảnh của điểm đó qua phép đối xứng trục d 3 trên hình ℋ.
Do đó phép đối xứng trục d 3 biến hình ℋ thành chính nó.
Vì vậy d 3 là trục đối xứng của hình ℋ.
Chứng minh tương tự với hai đường thẳng \({Đ_1},{\rm{ }}{Đ_2},\) ta được \({Đ_1},{\rm{ }}{Đ_2}\;\) cũng là trục đối xứng của hình ℋ.
Vậy hình ℋ có 3 trục đối xứng là các đường thẳng \({Đ_1},{\rm{ }}{Đ_2},{\rm{ }}{Đ_3}.\)
Do đó ta chọn phương án D.