Giải bài 3 trang 19 Chuyên đề học tập Toán 11 Chân trời sáng tạo
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 2), B(4; –3) và M(–8; 5).
Đề bài
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(3; 2), B(4; –3) và M(–8; 5).
a) Tìm ảnh của A qua \({Đ_{Ox}}\) và ảnh của B qua \({Đ_{Oy}}\) .
b) Biết M là ảnh của N qua \({Đ_{Oy}}\) . Xác định tọa độ của N.
Phương pháp giải - Xem chi tiết
Nếu \(M' = {Đ_{Ox}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = {x_M}\\{y_{M'}} = - {y_M}\end{array} \right.\)
Nếu \(M' = {Đ_{Oy}}(M)\) thì biểu thức tọa độ \(\left\{ \begin{array}{l}{x_{M'}} = - {x_M}\\{y_{M'}} = {y_M}\end{array} \right.\)
Lời giải chi tiết
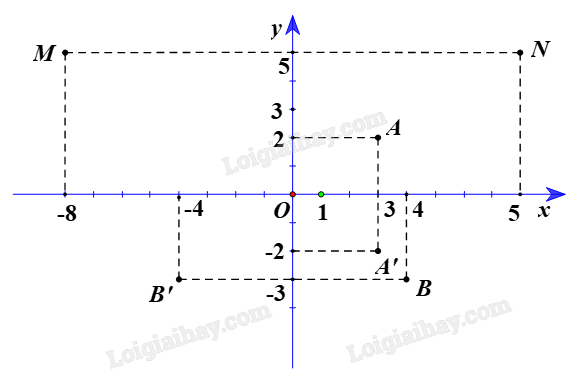
a)
+ Gọi A’ là ảnh của A qua \({Đ_{Ox}}\).
Suy ra Ox là đường trung trực của đoạn AA’ hay A’ đối xứng với A qua Ox
Do đó hai điểm A(3; 2) và A’ có cùng hoành độ và có tung độ đối nhau.
Vì vậy tọa độ điểm A’(3; –2).
+ Gọi B’ là ảnh của B qua \({Đ_{Oy}}\).
Suy ra Oy là đường trung trực của đoạn BB’ hay B’ đối xứng với B qua Oy
Do đó hai điểm B(4; –3) và B’ có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ điểm B’(–4; –3).
Vậy ảnh của A qua \({Đ_{Ox}}\) là A’(3; –2) và ảnh của B qua \({Đ_{Oy}}\) là B’(–4; –3).
b) Ta có M là ảnh của N qua \({Đ_{Oy}}\)
Suy ra Oy là đường trung trực của đoạn MN hay M và N đối xứng với nhau qua Oy
Do đó hai điểm M(–8; 5) và N có cùng tung độ và có hoành độ đối nhau.
Vì vậy tọa độ điểm N(8; 5).
Vậy tọa độ N(8; 5).