Giải Bài 3 trang 65 sách bài tập toán 7 - Chân trời sáng tạo
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Gọi H và K là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh rằng DH = DK.
Đề bài
Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Gọi H và K là chân các đường vuông góc kẻ từ D đến AB và AC. Chứng minh rằng DH = DK.
Phương pháp giải - Xem chi tiết
Chứng minh: \(\Delta A{\rm{D}}H = \Delta A{\rm{D}}K\)
Lời giải chi tiết
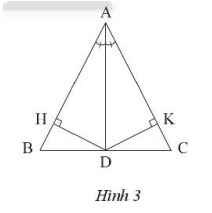
Xét hai tam giác vuông ADH và ADK có:
cạnh huyền AD chung
\(\widehat {BA{\rm{D}}} = \widehat {CA{\rm{D}}}\) ( vì AD là phân giác của góc A)
Suy ra: \(\Delta A{\rm{D}}H = \Delta A{\rm{D}}K\) (cạnh huyền – góc nhọn)
Suy ra: DH = DK
Cùng chủ đề:
Giải Bài 3 trang 65 sách bài tập toán 7 - Chân trời sáng tạo