Giải bài 3 trang 84 vở thực hành Toán 8 tập 2
Trong hình 9.1, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau.
Đề bài
Trong hình 9.1, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng
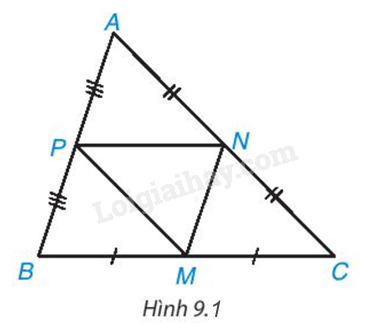
Phương pháp giải - Xem chi tiết
Dựa vào định lí để chứng minh hai tam giác đồng dạng.
Lời giải chi tiết
Xét tam giác APN và MNP, ta có:
$\widehat{APN}=\widehat{MNP},\widehat{ANP}=\widehat{MPN}$ (các góc tương ứng), PN là cạnh chung.
Vậy $\Delta APN=\Delta MNP\,(g.g)$. Tương tự $\Delta PBM=\Delta MNP,\Delta NMC=\Delta MNP$.
Do PN là đường trung bình của tam giác ABC nên PN // BC.
Suy ra $\Delta APN\backsim \Delta ABC$.
Vậy bốn tam giác APN, PBM, NMC, MNP đôi một bằng nhau và cùng đồng dạng với tam giác ABC. Do đó cả năm tam giác này đôi một đồng dạng với nhau.