Giải bài 31 trang 100 sách bài tập toán 11 - Cánh diều — Không quảng cáo

Đề bài

Cho hình chóp $S.ABCD$. Gọi ${\alpha _1}$, ${\alpha _2}$, ${\alpha _3}$, ${\alpha _4}$ lần lượt là góc giữa các đường thẳng $SA$, $SB$, $SC$, $SD$ và mặt phẳng $\left( {ABCD} \right)$. Chứng minh rằng $SA = SB = SC = SD \Leftrightarrow {\alpha _1} = {\alpha _2} = {\alpha _3} = {\alpha _4}$.

Lời giải chi tiết

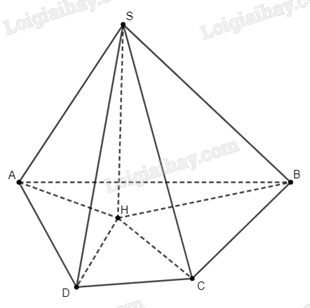
Gọi $H$ là hình chiếu của $S$ trên $\left( {ABCD} \right)$.

Dễ thấy rằng ${\alpha _1}$, ${\alpha _2}$, ${\alpha _3}$, ${\alpha _4}$ là những góc tạo bởi đường thẳng và mặt phẳng, nên chúng không lớn hơn ${90^o}$.

Vì $H$ là hình chiếu của $S$ trên $\left( {ABCD} \right)$, ta suy ra ${\alpha _1} = \widehat {SAH}$.

Tam giác $SAH$ vuông tại $H$, ta có $\sin {\alpha _1} = \sin \widehat {SAH} = \frac{{SH}}{{SA}}$.

Chứng minh tương tự, ta cũng có:

+ ${\alpha _2} = \widehat {SBH}$, $\sin {\alpha _2} = \sin \widehat {SBH} = \frac{{SH}}{{SB}}$,

+ ${\alpha _3} = \widehat {SCH}$, $\sin {\alpha _3} = \sin \widehat {SCH} = \frac{{SH}}{{SC}}$,

+ ${\alpha _4} = \widehat {SDH}$, $\sin {\alpha _4} = \sin \widehat {SDH} = \frac{{SH}}{{SD}}$,

Vậy,  $SA = SB = SC = SD \Leftrightarrow \frac{{SH}}{{SA}} = \frac{{SH}}{{SB}} = \frac{{SH}}{{SC}} = \frac{{SH}}{{SD}}$

$\Leftrightarrow \sin {\alpha _1} = \sin {\alpha _2} = \sin {\alpha _3} = \sin {\alpha _4} \Leftrightarrow {\alpha _1} = {\alpha _2} = {\alpha _3} = {\alpha _4}$.

Bài toán được chứng minh.