Giải bài 33 trang 102 sách bài tập toán 8 - Cánh diều
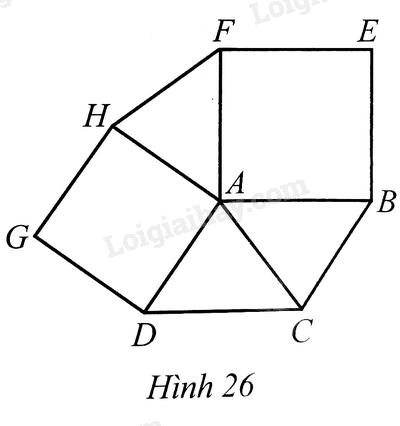
Cho hình bình hành \(ABCD\). Ở phía ngoài hình bình hành, vẽ các hình vuông \(ABEF\) và \(ADGH\) (Hình 26). Chứng minh:
Đề bài
Cho hình bình hành \(ABCD\). Ở phía ngoài hình bình hành, vẽ các hình vuông \(ABEF\) và \(ADGH\) (Hình 26). Chứng minh:
a) \(\Delta AHF = \Delta ADC\)
b) \(AC \bot HF\).
Phương pháp giải - Xem chi tiết
Dựa vào các trường hợp bằng nhau của tam giác và tính chất của hình vuông:
Trong một hình vuông,
- Các cạnh đối song song
- Hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.
- Hai đường chéo là các đường phân giác của các góc ở đỉnh.
Lời giải chi tiết
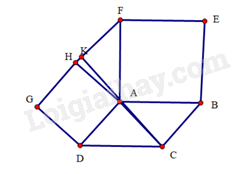
Gọi \(K\) là giao điểm của \(AC\) và \(HF\)
a) Do \(ABEF\) và \(ADGH\) đều là hình vuông nên\(\widehat {BAF} = \widehat {DAH} = 90^\circ ,AH = BA,AH = DA\)
Do \(ABCD\) là hình bình hành nên \(BA = DC\). Suy ra \(AF = DC\)
Ta chứng minh được \(\widehat {HAF} + \widehat {DAB} = 180^\circ \) và \(\widehat {ADC} + \widehat {DAB} = 180^\circ \)
Suy ra \(\widehat {HAF} = \widehat {ADC}\)
Xét hai tam giác \(HAF\) và \(ADC\), ta có: \(AH = DA,\widehat {HAF} = \widehat {ADC},AF = DA\)
Suy ra \(\Delta HAF = \Delta ADC\) (c.g.c)
b) Ta có: \(\widehat {HAK} + \widehat {DAH} + \widehat {DAC} = \widehat {CAK} = 180^\circ \) và \(\widehat {DAH} = 90^\circ \) nên \(\widehat {HAK} + \widehat {DAC} = 90^\circ \)
Mà \(\widehat {AHF} = \widehat {DAC}\) (vì \(\Delta HAF = \Delta ADC\)), suy ra \(\widehat {HAK} + \widehat {AHF} = 90^\circ \)
Trong tam giác \(AHK\), ta có: \(\widehat {AKH} + \widehat {HAK} + \widehat {AHF} = 180^\circ \). Suy ra \(\widehat {AKH} = 90^\circ \)
Vậy \(AK \bot HK\) hai \(AC \bot HF\).