Giải bài 34 trang 64 sách bài tập toán 8 - Cánh diều — Không quảng cáo

Đề bài

Cho hai hàm số \(y = x + 5;y =  - x + 1\).

a)     Vẽ đồ thị của hai hàm số đó trên cùng một mặt phẳng tọa độ.

b)    Gọi \(A\) là giao điểm của hai đường thẳng \(y = x + 5;y =  - x + 1\); \(B,C\) lần lượt là giao điểm của hai đường thẳng đó với trục \(Ox\). Tính diện tích của tam giác \(ABC\) (đơn vị đo trên các trục tọa độ là centimet).

Lời giải chi tiết

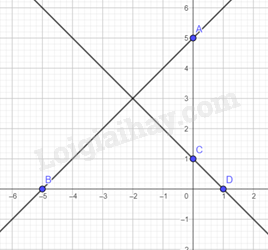
Xét đồ thị hàm số \(y = x + 5\), ta có:

Chọn \(x = 0\) suy ra \(y = 5\)

Chọn \(y = 0\) suy ra \(x =  - 5\)

Vậy đồ thị của hàm số \(y = x + 5\) là đường thẳng đi qua hai điểm \(A\left( {0;5} \right),B\left( { - 5;0} \right)\).

Xét đồ thị hàm số \(y =  - x + 1\), ta có:

Chọn \(x = 0\) suy ra \(y = 1\)

Chọn \(y = 0\) suy ra \(x = 1\).

Vậy đồ thị của hàm số \(y =  - x + 1\) là đường thẳng đi qua hai điểm \(C\left( {0;1} \right)\), \(D\left( {1;0} \right)\)

Vẽ đồ thị hàm số trên mặt phẳng tọa độ:

a)     Gọi \(H\) là hình chiếu của \(E\) trên trục \(Ox\)

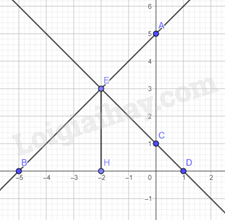
Ta có: \(E\left( { - 2;3} \right),B\left( { - 5;0} \right),C\left( {1;0} \right),H\left( { - 2;0} \right)\). Khi đó \(EH = 3cm\), \(BD = 6cm\)

Vậy diện tích của tam giác \(EBD\) là: \(\frac{1}{2}.3.6 = 9\left( {c{m^2}} \right)\).