Giải Bài 39 trang 81 sách bài tập toán 7 - Cánh diều
Cho tam giác ABC có AB = AC. Gọi D là trung điểm của BC. Vẽ CM vuông góc với AB tại M, BN vuông góc với AC tại N. Chứng minh AM = AN.
Đề bài
Cho tam giác ABC có AB = AC. Gọi D là trung điểm của BC. Vẽ CM vuông góc với AB tại M, BN vuông góc với AC tại N. Chứng minh AM = AN.
Phương pháp giải - Xem chi tiết
- Chứng minh ΔADB=ΔADC(c−c−c) suy ra ^ABC=^ACB hay ^MBD=^NCD
- Chứng minh ΔBNC=ΔCMB (cạnh huyền – góc nhọn) suy ra: AB = AC và BM = CN hay
AM = AN
Lời giải chi tiết
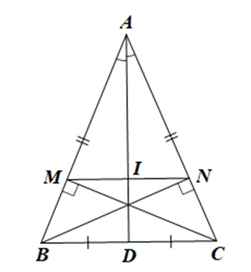
Xét ∆ABD và ∆ACD có:
AB = AC (giả thiết),
BD = CD (do D là trung điểm của BC),
AD là cạnh chung
Do đó ∆ABD = ∆ACD (c.c.c).
Suy ra ^ABD=^ACD hay ^MBC=^NCB.
Xét ∆BMC và ∆CNB có:
^BMC=^CNB(=90∘)
BC là cạnh chung,
^MBC=^NCB (chứng minh trên),
Do đó ∆BMC và ∆CNB (cạnh huyền – góc nhọn).
Suy ra BM = CN (hai cạnh tương ứng).
Ta có AB = AM + MB, AC = AN + NC.
Mà AB = AC, BM = CN.
Suy ra AM = AN.
Vậy AM = AN.